Tidevandsmålinger ved Hornbæk og Gedser 1891-2005 version I
| 25-04-2012 12:12 | |
| kfl★★★★★ (2167) |
Interesserede kan man læse mere om Cliff Olivers bedrifter KFL Vær skeptisk over for skeptikerne.... Det er der grund til. |
| Tidevandsmålinger ved Hornbæk og Gedser 1891-2005 version I25-04-2012 13:17 | |
| kfl★★★★★ (2167) |
Tidevandsmålinger ved Hornbæk og Gedser 1891-2005 version I – tilføjelser / link til graf opdateret Spørgsmålet er, om man kan identificere en periodisk bevægelse i vandstanden på 18,6 år ved Gedser efter man har fjernet den lineære trend i vandstandsstigningerne. Dette er undersøgt ved at optegne periodogrammet, autokorrelationen og de partielle autokorrelation. Disse grafer er værktøjer i tidsrække analyser til at identificere periodiske bevægelser og til at undersøge, hvilke ARIMA-model, der bedst beskriver data. Følgende figur viser disse grafer samt den årlige middelvandstand inkl. outliers. 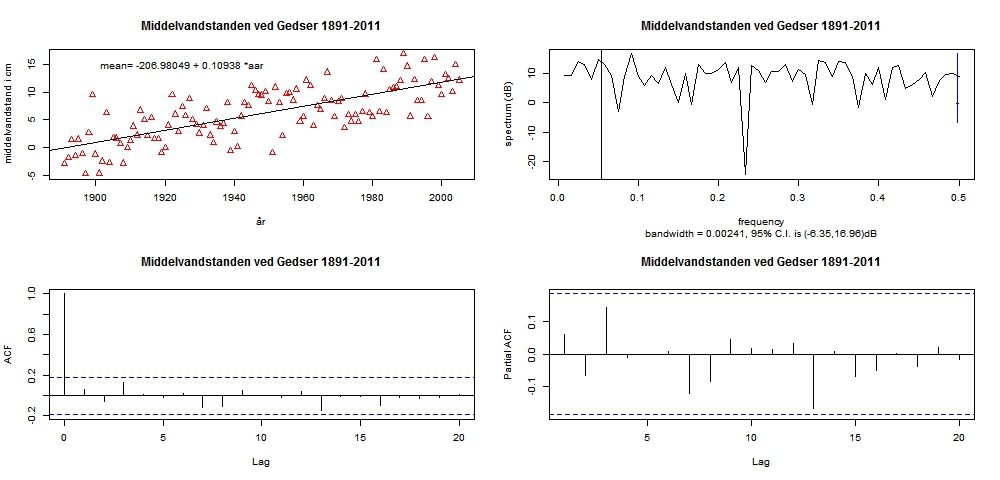 Af periodogrammet fremgår, at der ikke er markant spidser. Der er indtegnet en lodret line svarende til en periodisk bevægelse på 18,6 år. Dette betyder, at der ikke er nogen periodisk bevægelse på 18,6 år i data. Vi ved fra teorien om tidevand, at der er en periodisk bevægelse på 18,6 år, men den er åbenbart ikke så markant, at den slår igennem i denne analyse. Graferne ACF og Partielle ACF indikerer, at der kan anvendes en AR(1)-model til beskrivelse af restvariation, eller med andre ord: Vandstanden ved Gedser kan beskrives en lineær trend med en fejl, der har et års tømmermænd. I AR(1)-modellen fås årets værdi som en brøkdel af forrige års værdi plus et tilfældigt udsving - deraf betegnelsen "et års tømmermænd" . Der er ikke konstateret en acceleration i den årlige middelvandstand. KFL Vær skeptisk over for skeptikerne.... Det er der grund til. Redigeret d. 25-04-2012 13:19 |
| 25-04-2012 22:24 | |
| Kosmos★★★★★ (5371) |
Interesserede kan man læse mere om Cliff Olivers bedrifter - nå, jeg troede ellers ikke. du subskriberede på konspirationsteorier!? |
| 25-04-2012 23:03 | |
| SRJ★★★☆☆ (462) |
kfl skrev: Ud fra ACF og PACF graferne synes jeg ligeså godt det se ud til at restvariationen kan beskrives som en white noise proces. For en ARX-proces vil man forvente at ACF-grafen aftager løbende mens PACF-grafen går til nul efter lag X. Se f. eks. denne pdf side 3 hvor det diskuteres for specialtilfældet AR1. Hvilken værdi har den fittede AR1 parameter? Ud fra lidt eksperimenteren i R vil jeg gætte på at den er relativt lav. Ganske flot arbejde i øvrigt. |
| 26-04-2012 07:08 | |
| kfl★★★★★ (2167) |
@SRJ Tak for komplimentet. Det glædeligt, at der flere på Klimadebat, der kender noget til statistik og arima-processer. Her er resultat fra R_programmet: Call: Det er korrekt, at ar1 ikke er særlig stor og ikke signifikant forskellig fra nul. Jeg tror det er vanskeligt, at identificere 18,6 års cyklen i tidevandet ved de danske kyster. KFL Vær skeptisk over for skeptikerne.... Det er der grund til. Redigeret d. 26-04-2012 07:10 |
| RE: Beregning af tidevand – hjælp ønskes26-04-2012 11:28 | |
| kfl★★★★★ (2167) |
Beregning af tidevand – hjælp ønskes I forbindelse med analyser af vandstandsstigningerne ved Hornbæk og Gedser burde man ideelt set have adgang til tidevandsprognoserne, således at man kan eliminere tidevandsbevægelserne fra de egentlig vandstandsstigninger. Det er en kompliceret sag for lægmand at foretage disse beregninger. Hele teorien er velkendt og der findes programmer i MATLAB til dette, men dette program har jeg ikke adgang til og kender heller ikke nok til detaljerne i tidevandsberegning. Inspirationskilden til dette forslag stammer fra SEAFRAME-projektet, som den Australske regering har stået for. Mit forslag til fremgangsmåder er følgende: 1)Ud fra frekvensanalyse via periodogrammet skønnes over de vigtigste frekvenser 2)Ud fra de valgte frekvenser estimes en harmonisk sum Analyse af frekvenser Følgende graf viser periodogrammet for det tidevandet for Gedser for perioden 1910-1912 baseret på måling af tidevandet for hver time. 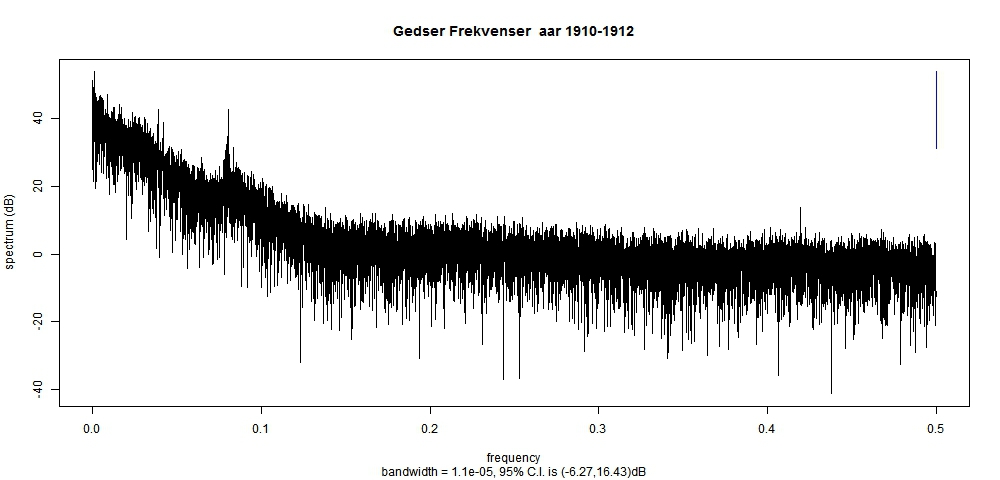 Denne graf viser, at der er en ophobning af frekvenser omkring 0,8 svarende til en perioder på ca. 12 timer. For at få en bedre opløsning plottes nu periodogrammet for mindre intervaller: 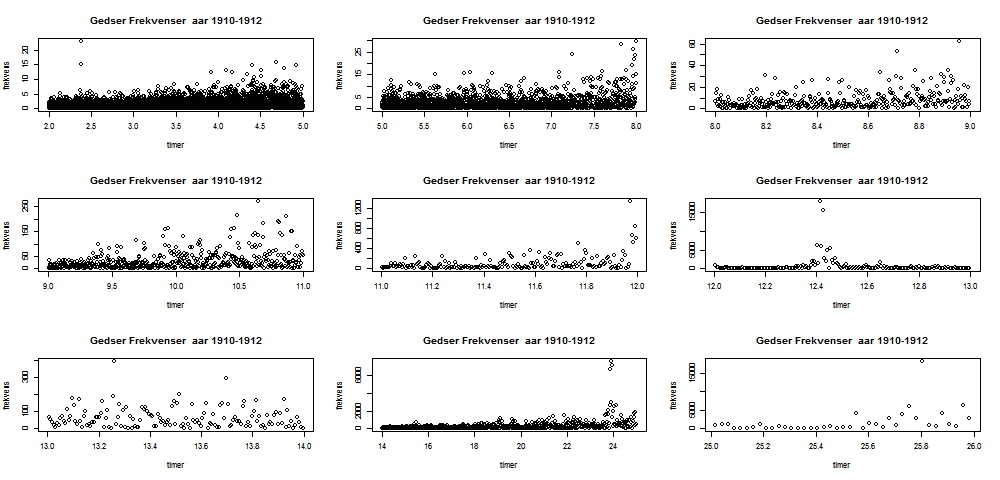 Estimation Ud fra disse grafer skønnes, at der er cykler med perioderne 12.0, 12.4, 24.0 og 25.8. De forskellig cykler i forbindese med tidvandsberegnner har for skellige navne, så som M2,S2,S1,etc, men som jeg ikke kender. Gad vide hvad navnene er på disse cykler: Cycle 12.0: S2 Cycle 12.4: M2 Cycle 24.0: S1 Cycle 25,8: ? Der estimeres derfor en harmonisk serie på 4 led af typen: a*cos(2*pi*t/periode)+b*sin(2*pi*t/periode)
Kun en mindre del af den samlede variation kan forklares ved en harmonisk sum. Tidevandsmålingerne og den estimerede kurve fremgår af følgende graf: 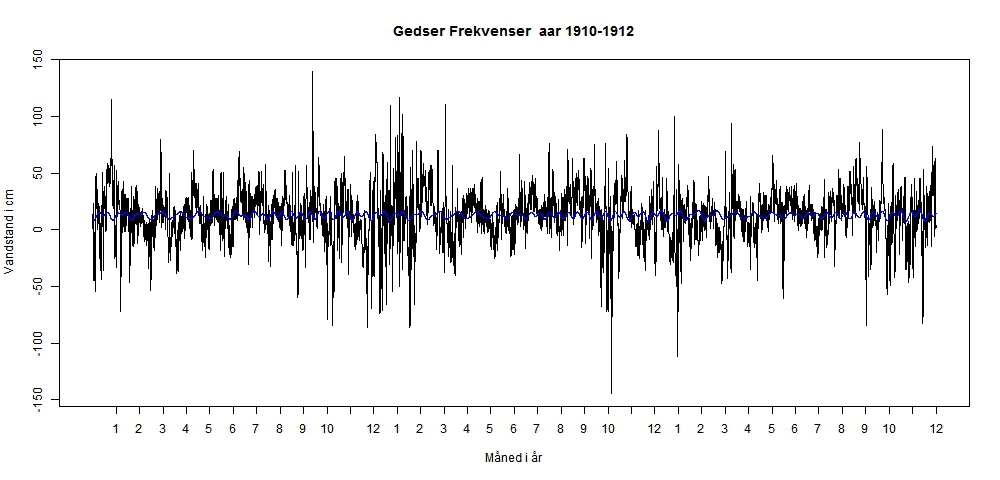 Den estimerede tidevandskurver er optegnet i følgende graf: 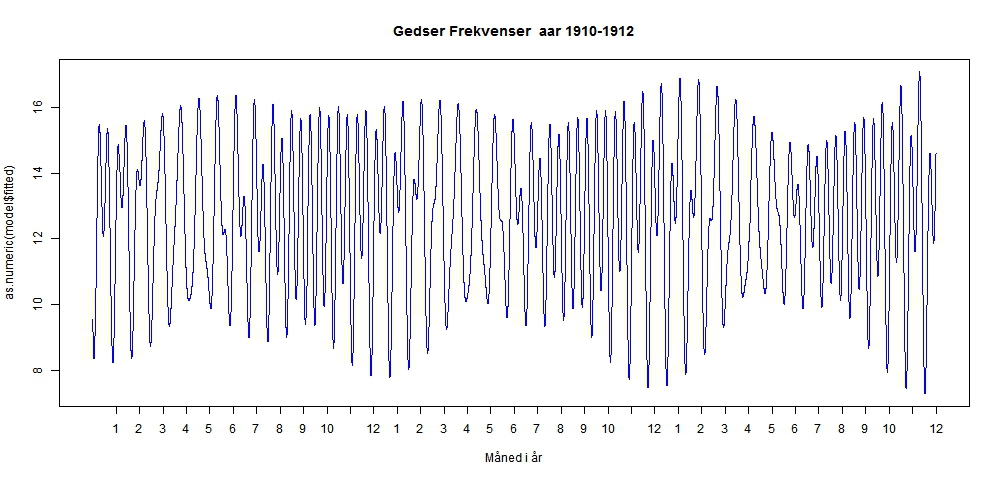 Langt størstedelen af variationen ligger ikke i tidevandsbevægelserne og må derfor ligge i vind, strøm og lufttryk. Tidevandet er kun ansvarlig for højst 10 cm i bevægelsen i vandstanden ifølge ovenstående beregning. Alternativt er der noget galt med den metode, som jeg anvender til beregning af tidvandet. Ser vi på hvad DMI's tidevandsprognoser fra den 26.april 2012, kommer man frem til en variation på ca. 10 cm. DMI Gedser Tidevand 26.april 2012. Det er muligt, at jeg er kommet frem til nogenlunde samme resultat som DMI, hvad angår det maksimal udsving i tidevandet, men metoden kan være helt forkert. Hvis jeg forsøger, at foretage beregningen for hele perioden 1891-2005, får jeg næsten samme periodogram med cyklerne 12.0, 12.4 og 24, men endnu mindre variation af det beregnede tidevand. 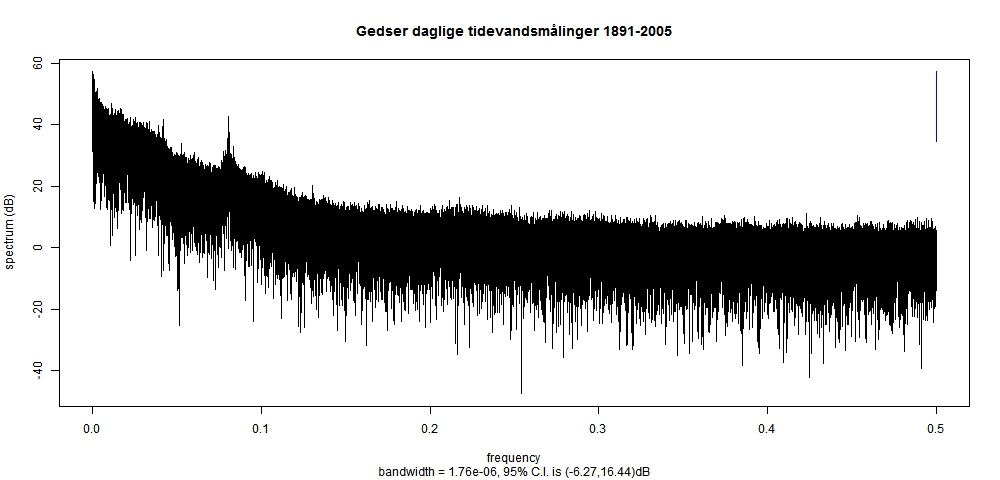 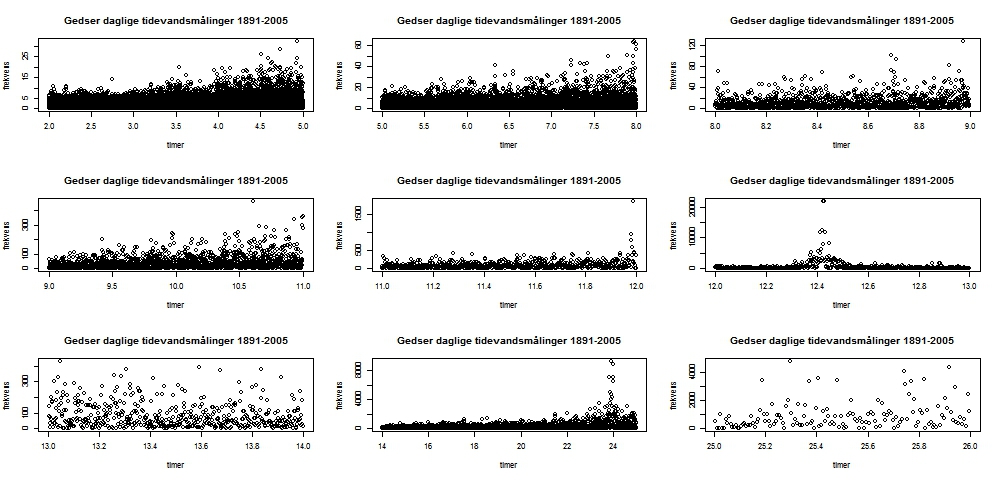 Det vil glæde mig, hvis der er nogle statistiknørder eller/og tidevandsnørder på Klimadebat.dk, der vil tage denne diskussion op. Kom hellere end gerne med alternative forslag til beregning af tidenvandet. KFL Vær skeptisk over for skeptikerne.... Det er der grund til. Redigeret d. 26-04-2012 12:11 |
| 26-04-2012 12:13 | |
| SRJ★★★☆☆ (462) |
kfl skrev: Jeg har i stedet for Matlab brugt Scilab som er gratis. Syntaksen er meget lig Matlabs og der er indbygget en oversættelsesfunktion til at oversætte Matlabs m-filer til Scilabs sci-filer. Det er muligt at du kunne oversætte de funktioner du har brug for og så bruge Scilab. Et andet alternativ til Matlab er Octave, men det har jeg ingen erfaring med selv. Hvilken R-funktion benytter du til at udregne periodogrammet?
Umiddelbart virker din metode fornuftig - har dog ikke selv erfaring med tidevandsberegninger. Resultatet er også i overenstemmelse med det man forventer for tidevandet i Østersøen som er på 5-15 cm. Se f. eks. her: http://vejret.tv2.dk/artikel/id-47261564:derfor-får-vi-så-kraftigt-højvande.html?ss hvor der også diskuteres hvordan vindens påvirkning giver en "badekar" effekt i Østersøen Når amplituden af tidevandsudsvinget er så lav ifht. andre faktorer som f. eks. vind og strøm forklarer det jo nok også hvorfor 18.6 års perioden ikke kan ses i denne dataserie. |
| 26-04-2012 12:18 | |
| kfl★★★★★ (2167) |
Hej SRJ Her er den kode jeg benytter til at danne grafer og beregne periodogramme, idet tvand indeholder tidevandsdata for Gedser: aar<-1910:1912 aar_txt<-" aar 1910-1912" attach(tvand) par(mfrow=c(1,1)) ix<-year %in% c(aar) a<-spectrum(cmadj[ix],log="dB",plot=T,main=paste(fil_3,aar_txt)) detach(tvand) KFL Vær skeptisk over for skeptikerne.... Det er der grund til. |
| 26-04-2012 12:28 | |
| SRJ★★★☆☆ (462) |
Hej kfl Jeg fandt lige en R-pakke der er lavet til oceanografisk data-analyse: http://cran.r-project.org/web/packages/oce/index.html Den indeholder funktionen tidem() som muligvis kan det du er ude efter, men funktionen er under udvikling iflg. manualen. Derudover indeholder pakken funktionen pwelch til at udregne dataseriens spektrum vha. Welch's metode. I denne metode deler man dataserien op i en række undervinduer og udregner spektret for hver af dem. Herved reduceres støjen i det estimerede spektrum men frekvensopløsningen bliver dårligere. |
| 26-04-2012 12:47 | |
| kfl★★★★★ (2167) |
Tak for vinket. Jeg har set denne pakke , men er ikke gået igang med den, idet jeg ikke ved pt hvorledes man får oprettet data så pakke kan anvendes. KFL Vær skeptisk over for skeptikerne.... Det er der grund til. |
| 26-04-2012 15:02 | |
| Kjeld Jul★★★★★ (3888) |
Hej KLF Tak fordi,du henviste til IPCC tilhængernes web site,så kan interesserede da læse de mange indlæg,som skeptikkere til den gængse CO2 teori er kommet med,som man kan se,er de ikke alle sammen lægfolk og armatører. Uanset hvormeget IPCC tilhængerne forsøger,at miskreditere videnskabsmænd og forskere,som har en anden mening om årsagen til klimaforandringerne,er den globale temp. ikke steget i mere end 10 år,havvandet er blevet koldere og havvandsstigningsraten er faldende,havisens udbredelse i polarhavet og omkring Antarktis er nu næsten normal for årstiden. Ingen af IPCCs prognoser er blevet opfyldte,heldigvis da,så havde vi vel allerede idag gået i vand til knæene,polarhavet havde været isfrit og isbjørnene kunne vi læse om i historiebøgerne. Jeg er klimarealist og tror på solen,oceanerne og skyerne,som primært årsagen til klimaforandringerne. |
| 26-04-2012 15:55 | |
| kfl★★★★★ (2167) |
Hej Kjeld Vi har forskellige synspunkter vedr. klimaet. Jeg har baseret mig på en videnskabelig tilgang og du har valgt en anden. Det er OK. Derfor behøver vi to ikke at bruge tid på at debattere emnet med hinanden fremover og heller ikke at tale nedsættende om hinanden jf. nogle grelle eksempler her på siden. Jeg vil forsat deltage i debatten og bidrage med den viden jeg har /ikke har om klimaet. KFL Vær skeptisk over for skeptikerne.... Det er der grund til. Redigeret d. 26-04-2012 15:59 |
| 26-04-2012 16:43 | |
| SRJ★★★☆☆ (462) |
SRJ skrev: Jeg har brugt lidt tid på at forstå pakken og de to funktioner. pwelch er nem at bruge, enten på en liste af numre eller et ts-objekt i R. Men dokumentationen af funktionen er ikkw nøjagtig, f. eks. er window=4 som default, ikke 8 som der står i manualen. Desuden er outputtet ikke standard, frekvensen gives som normaliseret frekvens- man skal derfor gange med sample frekvensen. Værdierne for spektret er heller ikke normaliserede, for at få noget der ligner resultatet fra R's spectrum skal man dividere outputtet fra pwelch med N, N antal punkter: Fs <- 1000 #sample frequency t <- seq(0, 0.296, 1/Fs) x <- cos(2 * pi * t * 200) + rnorm(n=length(t)) xts <- ts(x, frequency=Fs) s <- spectrum(xts, spans=c(3,2), main="random + 200 Hz", log="no") w <- pwelch(xts, plot=FALSE ) lines(w$freq*Fs, w$spec/(297), col="red") abline(v=200, col="blue", lty="dotted") #lodret linie for 200 Hz Funktionen tidem() laver harmonisk analyse ved at fitte vandstanden til en sum af sinus og cosinus termer for en række standard tide-frekvenser som de er givet af Foreman i denne manual. Hvor mange frekvenser der benyttes afhænger af hvor lang dataserien er, se tabel 5 i pdf'en. Pakken oce indeholder også funktionen as.sealevel() som kan bruges til at konvertere en R vektor til et sealevel object der derefter kan fittes med tidem(). Jeg har fundet et eksempel i manualen og modificeret det lidt så man det lidt ligner tilfældet fra Gedser. Dvs. der er en stor variation i vandstanden som den harmoniske model ikke medtager - se tilknyttet figur. # sequence of 10 days t <- seq(0, 10*86400, 3600) # time in sec, increments of 3600 s=1 hour T <- 1/0.080511401 # tidal period eta <- sin(1/T * t * 2 * pi / 3600)/4 +1* rnorm(n=length(t)) sl <- as.sealevel(eta) time <- sl[["time"]] elevation <- sl[["elevation"]] oce.plot.ts(time, elevation, type="l", ylab="Height [m]", ylim=c(-2,6)) legend("topleft", legend=c("Test data","Detided"),col=c("black","red"),lwd=1) tide <- tidem(sl, constituents) detided <- elevation - predict(tide) lines(time, detided, col="red") plot(eta, type="l"); lines(predict(tide), col=2) legend("topleft", legend=c("Testdata","Tide"),col=c("black","red"),lwd=1) summary(tide) Man kan vælge hvilke tidefrekvenser der skal medtages i analysen ved at specificere dem i kaldet til tidem: tide <- tidem(sl, constituents=c("K1", "M2")) Der er også diverse bugs med denne funktion, f. eks. kan man ikke se outputtet med kommandoen summary.tidem som tilsyneladende mangler. En liste over de fittede parametre fås istedet med R's summary. Hvis du bruger funktionen på hele dataserien så vil det nok tage ret lang tid, den virker ret langsom. Tilknyttet billede: 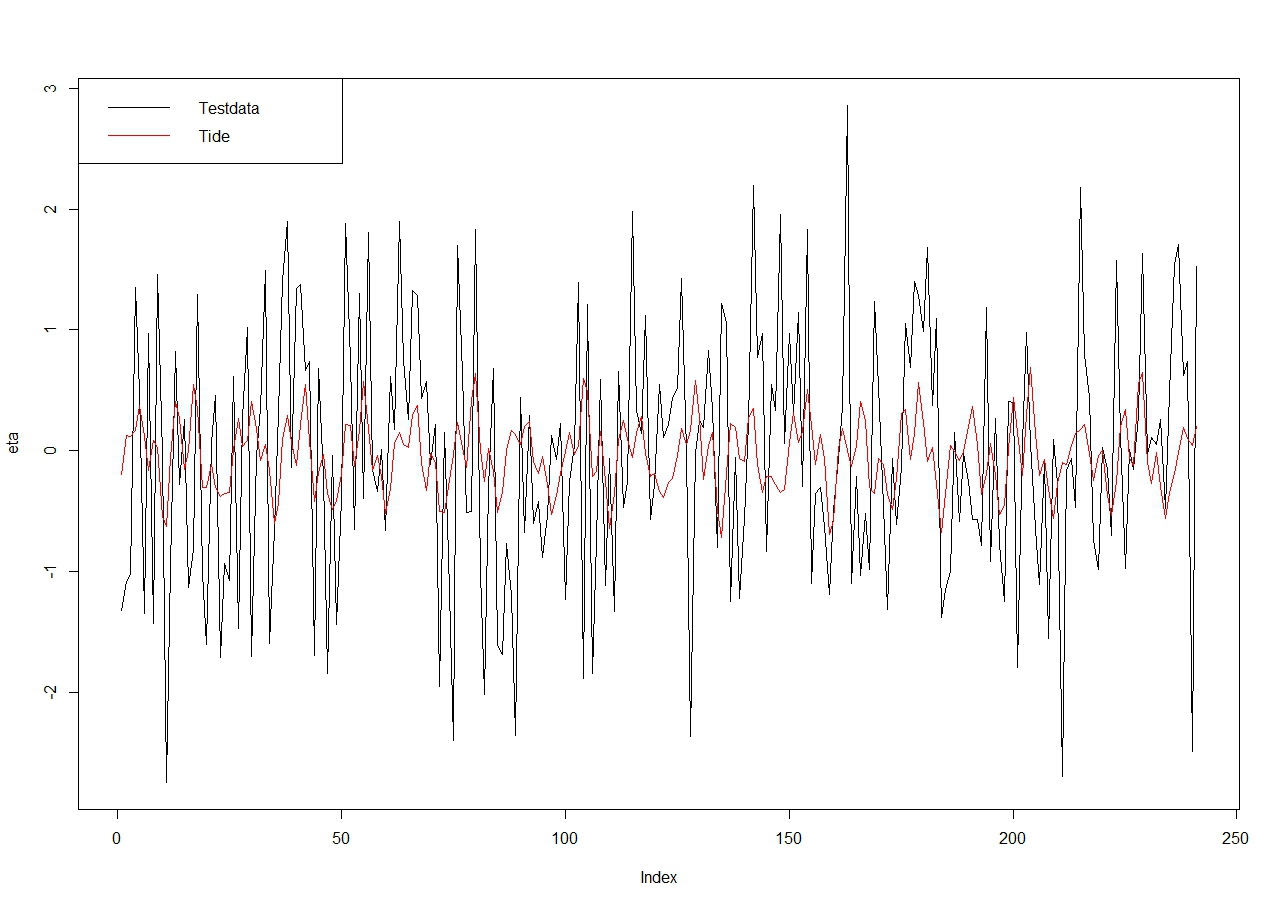
Redigeret d. 26-04-2012 16:47 |
| RE: Tak for hjælpen26-04-2012 17:18 | |
| kfl★★★★★ (2167) |
Tak for hjælp både mht. link til manualen og til R-kode. Det ser ud til, at du er en erfaren herre mht. både statistik og R-programmering. Jeg var begyndt at se på pwelch , men gik i stå på "tidem". Jeg studerede tidsrækkeanlyser for ca 35 år siden og er imponeret over, hvor meget R kan. Det er ganske sjovt at genopfriske gammel viden. Er du statistiker ? Jeg bruger SAS på arbejde i dag , men er tidligere en APL-nørd. Når jeg går på pension, har jeg ikke længere adgang til SAS. Derfor er jeg begyndt på at arbejde i R i hvert til klima-analyser og måske også på arbejde. KFL Vær skeptisk over for skeptikerne.... Det er der grund til. Redigeret d. 26-04-2012 17:19 |
| 27-04-2012 00:03 | |
| SRJ★★★☆☆ (462) |
Jeg er ikke statistiker men geofysiker (i gang med kandidat-delen). Indenfor geofysikken har jeg fokuseret på den indre jords geofysik, bl.a. seismologi og geomagnetisme (hvor jeg brugte Welch's metode i forbindelse med en opgave). Mht. klima har jeg kun haft det obligatoriske pensum på bachelor-delen, så det er ikke ret meget. Statistik har jeg lært henad vejen efter behov og på et enkelt kursus i anvendt statistik - hvor underviseren var eksperimentel partikelfysiker. Jeg lært en del yderligere statistik ved at forsøge at replikere visse af Taminos analyser, og det er bl. a. også der igennem jeg har lært mig selv at bruge R. Derudover har jeg efterhånden læst/skimmet en del bøger om statistik og anvendelser i geofysikken. Da jeg er selvlært i R, støder jeg ofte på diverse problemer. F. eks.forsøgte jeg at indlæse tidevandsdata for Gedser men fik problemer pga. formatet af datafilen. For de tidspunkter hvor vandstanden er et 3-cifret tal er der ikke et mellemrum mellem tidspunktet og målingen: 1892010523-105 Hvis jeg bruger flg. kommando ignores disse linier: d <- read.table("tr07-09/gedser.dat", fill = TRUE) men så mister jeg så de data. Jeg kan få det til at virke ved at bruge kommandoen d <- read.fwf("tr07-09/gedser.dat", widths=c(10,4), n=100000) Den kommando er dog umådelig langsom, så jeg har valgt maksimalt at indlæse 100000 punkter. Det er data for ca. 12 år så den længste periode jeg kan finde er ca 6 år. Ved brug af pwelch nedsættes frekvensopløsningen yderligere så for at have en chance for at se 18.6 perioden med Welch's metode skal der bruges en del mere data end for 2 perioder, dvs. mere data end for 37.2 år. Hvilke kommandoer bruger du for at indlæse filen? |
| 27-04-2012 00:08 | |
| SRJ★★★☆☆ (462) |
SRJ skrev: Ved nærmere eftertanke, så er det korrekt som der står i manualen, men det er lidt forvirrende, for window som man angiver i funktionen betyder hvor mange vinduer der laves på det halve frekvensinterval. Så der bliver det dobbelte antal. |
| 27-04-2012 14:23 | |
| Kjeld Jul★★★★★ (3888) |
Hej kfl. Jeg vil selvfølgelig også fremover følge debatindlæggene,og give mit bidrag til diverse emner. At vi ikke har samme holdning og opfattelse om årsagen til klimaforandringerne,ville aldrig foranledige mig til at bruge ukvemsord og nedsættende bemærkninger,hverken overfor dig eller andre i dette forum. Vi har alle vores specielle force og interesse,som vi på demokratisk vis har mulighed for at give tilkende i dette forum. |
| 27-04-2012 17:00 | |
| kfl★★★★★ (2167) |
@Kjeld Jul Godt svaret! KFL Vær skeptisk over for skeptikerne.... Det er der grund til. Redigeret d. 27-04-2012 17:00 |
| 27-04-2012 17:27 | |
| kfl★★★★★ (2167) |
Hej SRJ Det er også Tamino, der har inspireret mig mht. at anvende R. Jeg har lejet lidt med "tidem" funktionen, men kan kun foretage beregningen for ca 20 år ad gangen pga. af pladsproblemer. Derfor bliver jeg nødt til at loop og beregne tidevanden for hver år. Problemet er i mindre omfang at kunne køre programmet - langt større er at forstå og at efterkontrollere resultaterne. Programmet kan tilsyneladende ikke klare at beregene 18.6 års cyklen. Har du eller andre noget ide om hvad en teoretisk beregning af tidevandet's 18.6 års cyklen betyder for tidevandet for danske stationer ? Det var noget bøvlet noget at indlæse data, idet der var et par data fejl samt at jeg skulle regne frem og tilbage mellem julian og gregorian day number. Endelig skulle programmet også til læse både Gedser , Hornbæk og stormdata. Først førte gemte jeg data på min egen PC og rettet de få fejl. Det voldte mig problemer at tage hensyn til huller i data når varighed af en oversvømmelse skulle identificeres og at identificere oversvømmelsestyper. Fik ikke løst dette sidste. ##################################################################################### ### hornbaek_gedser_init_vandstand_data ## ##################################################################################### rm(list=ls()) options(digits=10) grafik_flag<-0 grafik_sti<-"c:\\Users\\Documents\\R_bibtek\\R_data\\Danske_Tidevandsmålinger\\" ######################################################################### #### Converter fra Gregorian to Julian data ### #### Se http://en.wikipedia.org/wiki/Julian_day#cite_note-13 ### ######################################################################### kfl.julian<-function(x){ yyyy<- x %/% 10000 mm<-(x %/% 100)-100*yyyy dd<-x - yyyy*10000-100*mm a<-(14-mm) %/% 12 y<-yyyy+4800-a m<-mm+12*a-3 jdate<-dd+((153*m+2) %/% 5)+365*y+(y %/% 4)-(y %/% 100)+(y %/% 400)-32045 jdate } kfl.julian(20000101) kfl.gregorian<-function(jd){ j<- jd j<- j+32044 g<- j %/% 146097 dg<-j %% 146097 c<-((dg %/% 36524+1)*3) %/% 4 dc<-dg-c*36524 b<-dc %/% 1461 db<-dc %% 1461 a<-((db %/% 365 +1)*3) %/% 4 da<-db-a*365 y<-g*400+c*100+b*4+a m<-((da*5+308) %/% 153) - 2 d<-da-(((m+4)*153) %/% 5)+122 y<-y-4800+((m+2)%/% 12) m<-(m+2) %% 12 +1 d<-d+1 yyyymmdd<-10000*y+100*m+d yyyymmdd } kfl.gregorian_yyyymmdd<-function(x){ mm_navn<-c("jan","feb","mar","apr","may","jun","juli","aug","sep","oct","nov","dec") n<-length(x) ud<-"" for (i in 1:n){ yyyy<-x[i] %/% 10000 mm<-(x[i]-10000*yyyy) %/% 100 dd<-(x[i]-10000*yyyy)-100*mm tmp<-paste(dd,mm_navn[mm],yyyy,sep="") ud<-c(ud,tmp) } ud<-ud[-1] ud } a<-kfl.gregorian_yyyymmdd(c(20120514, 20051224,18910523)) ##################################################################### ### Henter storm data ### ###################################################################### sti<-"c:\\Users\\Documents\\R_bibtek\\R_data\\Danske_Storme\\" setwd(sti) storme<-read.table("storme.raa.txt",header=T) antal_storme<-dim(storme)[1] grafik_flag<-0 grafik_sti<-"c:\\Users\\Documents\\R_bibtek\\R_data\\Danske_Tidevandsmålinger\\" retning_txt<-c("Ikke oplyst","Nordøst","Øst","Sydøst","Sydvest","Vest","Nordvest") ################################################################################ ### Læser data pege pind ### ############################################################################## fil_peger<-2 if (fil_peger==1) { fil<-"gedser.dat" fil.txt<-"Gedser daglige tidevandsmålinger 1891-2005" fil.txt.short<-"Gedser tidevandsmålinger" fil_1<-"Gedser_timelig.txt" fil_2<-"Gedser_aarlig.txt" } if (fil_peger==2){ fil<-"hornbaek.dat" fil.txt<-"Hornbæk daglige tidevandsmålinger 1891-2005" fil.txt.short<-"Hornbæk tidevandsmålinger" fil_1<-"Hornbaek_timelig.txt" fil_2<-"Hornbaek_aarlig.txt" } fil_1 fil_2 url<-paste("c:\\Users\\Documents\\R_bibtek\\R_data\\Danske_Tidevandsmålinger\\tr07-09\\",fil,sep="") antal<--1 tmp<-readLines(url,n=antal) n<-length(tmp) mat<-matrix(rep(0,10*n),ncol=10) mat[,1]<-as.numeric(substr(tmp,1,10)) mat[,7]<-as.numeric(substr(tmp,11,14)) mat[,2]<-mat[,1] %/% 1000000 mat[,3]<-mat[,1] %/% 10000 - mat[,2]*100 mat[,4]<-mat[,1] %/% 100 - mat[,2]*10000-mat[,3]*100 mat[,5]<-mat[,1] %% 100 mat[,6]<-kfl.julian(mat[,1] %/% 100)+(mat[,5]/24) model<-lm(mat[,7] ~ mat[,6]) summary(model) mat[,8]<-mat[,7] -(model$coef[1]+model$coef[2]*mat[,6])+(model$coef[1]+model$coef[2]*(kfl.julian(20051231)+12/24)) mat[,9]<-c(0,round(24*(mat[2:n,6]-mat[1n-1),6])-1)) mat[,10]<-round(mat[,6],0) ### Fletter stormdato på #### ### for (i in 1:n){ ### for (j in 1:antal_storme){ ### if (mat[i,10]!=storme[j,4]){mat[i,10]<-0} ### if ((i %/% 100)==0){print(paste(n,antal_storme,i,j))} ### } ### } colnames(mat)<-c("gregorian_","year","month","day","time","julian_","cm","cmadj","sl","storm") tvand<-data.frame(mat) #################################################################################### ### Finder års min,mean,max, ### #################################################################################### attach(tvand) f.max<-function(year,cm){ aar<-unique(floor(year)) n<-length(aar) year.resume<-matrix(rep(0,7*n),ncol=7) for (i in 1:n){ year.resume[i,1]<-aar[i] year.resume[i,2]<-min (cm[floor(year)==aar[i]]) year.resume[i,3]<-mean(cm[floor(year)==aar[i]]) year.resume[i,4]<-max (cm[floor(year)==aar[i]]) year.resume[i,5]<-sum (floor(year)==aar[i]) year.resume[i,6]<-mean(cmadj[floor(year)==aar[i]]) year.resume[i,7]<-year.resume[i,4]-year.resume[i,2] } year.resume } a<-f.max(year,cm) colnames(a)<-c("aar","min_cm","mean_cm","max_cm","antal","mean_cmadj","max_min") aarlig<-data.frame(a) detach(tvand) file<-paste("c:\\Users\\Documents\\R_bibtek\\R_data\\Danske_Tidevandsmålinger\\",fil_1,sep="") write.table(tvand,file,col.names=T,row.names=F) file<-paste("c:\\Users\\Documents\\R_bibtek\\R_data\\Danske_Tidevandsmålinger\\",fil_2,sep="") write.table(aarlig,file,col.names=T,row.names=F) Første version af programmet er OK, men det gode er næste version af programmet bliver langt bedre. Jeg kan evt sende koden+ koden for analyser programmer til en tekstfil. KFL Vær skeptisk over for skeptikerne.... Det er der grund til. Redigeret d. 27-04-2012 17:30 |
| 27-04-2012 23:54 | |
| SRJ★★★☆☆ (462) |
Tak for koden, det var lidt hurtigere end mit eget forsøg. Jeg har forsøgt at identicere 18.6 års cyklen i de årlige middelværdier som dit program udregner. Med lidt god vilje og ved at indstille antal vinduer og padding-faktoren kan jeg godt få periodogrammer med en top for den relevante frekvens. Se tilknyttet figur - grafen er i lidt dårlig kvalitet så man er nødt til at klikke på den så den forstørres for at se den ordentligt. Kode: library(oce) d <-read.table("tr07-09\\Gedser_aarlig.txt", skip=1) colnames(d)<-c("aar","min_cm","mean_cm","max_cm","antal","mean_cmadj","max_min") xts <- ts(d$mean_cmadj-1*mean(d$mean_cmadj), start=1891,freq=1) s <- spectrum(xts, pad=4, main="Spectrum of Gedser annual", log="no", plot=FALSE) w <- pwelch(xts, pad=1, window=1, plot=FALSE ) w2 <-spec.univar(xts,taper=0.05,spans=2,pad=4,confint=0.95, fast=TRUE) plot(w$freq, w$spec, col="red", type="l", log="yx", xlim=c(0.002,0.25) ) lines(w2$freq, w2$spec, col="green", type="l", log="xy", ylim=c(0.2,50) ) lines(s$freq, s$spec, col="black", type="l") abline(v=1/18.6, col="blue", lty="dotted") legend("bottomleft", legend = c("spectrum","spec.univar", "pwelch","18.6 yr"),bty = "n", col = c("black","green","red","blue"), lty = c(1,1,1,3) ) Tilknyttet billede: 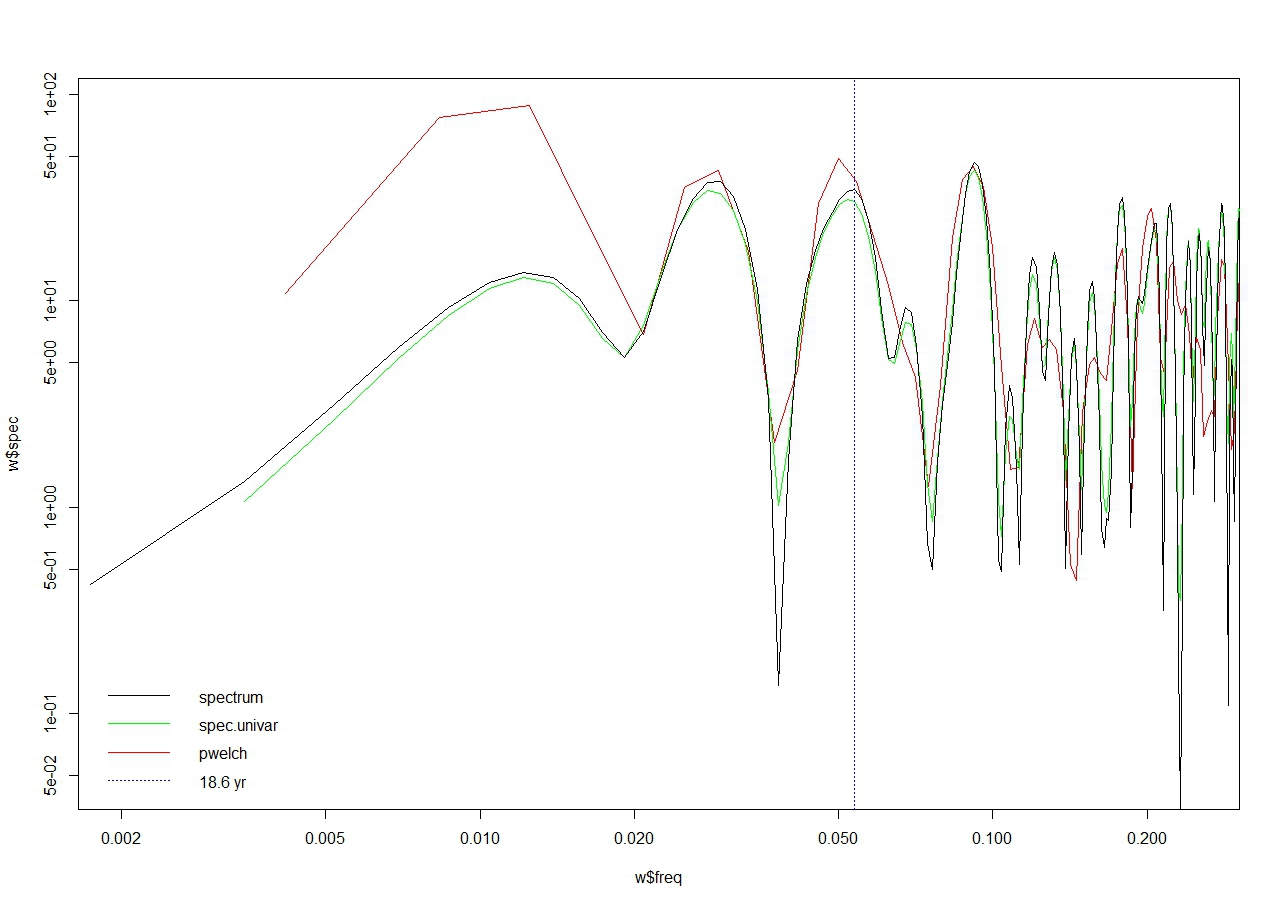
Redigeret d. 27-04-2012 23:55 |
| RE: local sea level 18.6 cycle28-04-2012 13:24 | |
| kfl★★★★★ (2167) |
Jeg stillede spørgsmålet: Har du eller andre noget ide om hvad en teoretisk beregning af tidevandet's 18.6 års cyklen betyder for tidevandet for danske stationer ? og har fundet et delvist svar, der antyder størrelsesordenen . The Effect of the 18.6-Year Lunar Nodal Cycle on Regional Sea-Level Rise Estimatest Abstract Som jeg læser dette har 18.6 cykle en påvirkning af amplityde på ca 2.2 cm global set. Hvad den så er i de indre danske farvande vides ikke. Søger videre for at finde et svar. KFL Vær skeptisk over for skeptikerne.... Det er der grund til. Redigeret d. 28-04-2012 13:31 |
| RE: Tidevandsmålinger ved Hornbæk og Gedser 1891-2005 version I – 18.6 års cyklen18-05-2012 12:40 | |
| kfl★★★★★ (2167) |
Tidevandsmålinger ved Hornbæk og Gedser 1891-2005 version I – 18.6 års cyklen Jeg har tidligere rejst spørgsmålet om der var nogle klimanørder eller tidvandsnørder, der har undersøgt hvor stor amplituden er på 18,6 års -cyklen. DMI er forespurgt, men de kunne ikke umiddelbart angive en størrelsesorden af amplituden for de berørte tidevandsstationer. Jeg har fået hjælp fra SRJ i form af link og bemærkninger. Imidlertid lå løsningen lige til højrebenet, idet jeg fandt følgende artikel The Effect of the 18.6-Year Lunar Nodal Cycle on Regional, hvor der direkte er anvist en metode til at finde effekten af 18,6 års-cyklen. Desuden har følgende præsentation relevans i relation til den geografisk variation af amplituden af 18,6 års cyklen Modelling global influences of the 18.6 . Der er flere grafer i denne præsentation, der viser betydningen/størrelsesordene af amplituden af 18,6 år cyklen over hele kloden. Der foregår tilsynelaende en omfattende forskningsaktivitet vedr. 18,6-års cyklen. Ifølge den første kilde kan den årlige middelvandstand beskrives ved: T(t)=A0+A1*t+A2*t^2+ A*cos(2*pi*t/18.6)+ B*sin(2^pi*t/18.6) Ud fra middelvandstanden for 6 hollandske tidevandsstationer for perioden 1890-2008 har forfatterne skønnet, at amplitude er på ca. 1,2 cm. Det er muligt ud fra DMI's fremragende data for Gedser og Hornbæk for perioden 1891-2005, at foretage samme analyse. Jeg har fundet følgende: Hornbæk: Amplitude af 18,6 års cyklen = 1,45 cm Stigning pr. 100 år = 2,44 cm Gedser: Amplitude af 18.6 års cyklen = 0,95 cm Stigningen pr. 100 år = 10,9 cm Amplituden for 18,6 årscyklen er ikke signifikant forskellig fra 0. Denne amplitude skal sammenlignes med amplituden af det daglige tidevand og den maksimale vandstand som følge af tidevand, vind, strøm og ændringer i lufttrykket etc. I meget runde tal gælder Samlet amplitude af ændringer i vandstanden: ca 200 cm Amplitude af tidevandet ca 30 cm Amplitude af 18,6 års cyklen ca 2 cm Dette betyder, at det normale tidevand bidrager med ca. 15 % og tidevandet fra at 18,6 års cyklen bidrager med ca. 1 % af det maksimal udsving i vandstanden. Som en tommelfingerregel for vandstanden ved Gedser og Hornbæk gælder, at 18,6 års-cyklen bidrager med ca. 1 % af udsvingene i vandstanden. Hvad kan gå galt, hvis man ikke tager hensyn til 18,6 års cyklen ved beregning af tidevandet? Af følgende figur fremgår, at hvis man ser på en kort periode på under 10 år, kan man finde en acceleration eller en de-acceleration svarende til at grafen er konveks eller konkav afhængigt af hvornår man starter en måleserie. 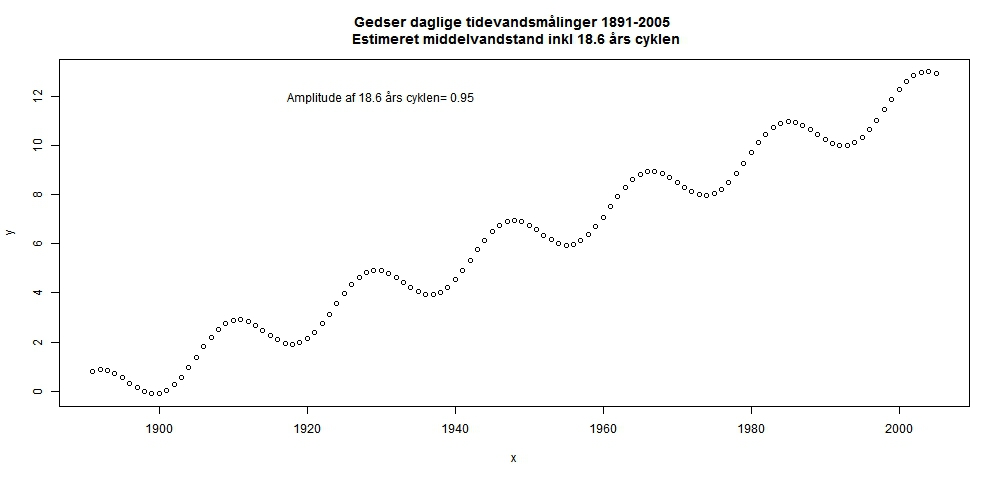 Hvis man ser på en længere periode, vil amplituden 18,6 års-cyklen blive udglattet, men til gengæld vil variansen vokse. Disse iagttagelser bevirker, at sattelit-målingerne af vandstanden giver, hvis den er kalibreret korrekt, et sandt billede af vandstanden lokalt, men skal være man skal være forsigtig med at bruge sattelit-vandstandsmålinger lokalt til at beregne en acceleration af vandstanden. Det er netop det den først nævnte kilder siger og hvad Jens Morten Hansen gentager. Dog går han over stregen ved at hævde, at han vandstandstiginger, som han har set i havet omkring Danmark, også vil gælde de næste 100 år. 18,6-årscyklen ændrer ikke ved den globale vandstand, idet den kun bevirker en omfordeling af vandet i verdenshavene. Desuden er det areal af verdenshavene, der er påvirket væsentlig af 18,6 års-cyklen meget begrænset. Det drejser sig primært om det nordvestlige Stillehave og SydØst Asien. Det ville være rart, hvis nogle af DMI's tidevandsnørder ville verificere resultatet for Hornbæk og Gedser. Hvis det viser sig, at ingen i DMI har forsøgt at estimere amplituden 18,6 års-cyklen for Geser og Hornbæk , er det godt gået af kfl. Der tages forbehold for fejl om mangler og at der kommer en opdateret version på et tidspunkt i henhold til de bemrækninger,der kan komme på kilamdebat. KFL Vær skeptisk over for skeptikerne.... Det er der grund til. Redigeret d. 18-05-2012 12:44 |
| 18-05-2012 15:39 | |
| SRJ★★★☆☆ (462) |
kfl skrev: Følgende gælder handler kun om data fra Gedser: Så var jeg på rette spor, jeg har allerede forsøgt lidt i den retning. Der forsøgte jeg at tilpasse harmoniske modeller til de årlige gennemsnit af "mean_cmadj". Jeg formoder at den model du viser i dit indlæg er baseret på et fit til "mean_cm". Her følger mine resultater for "mean_cm". Hvis jeg fitter en model med en kvadratisk og linear tidsafhængighed til "mean_cm" og en harmonisk svingning med periode på 18.6 år finder jeg: Model 1 coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.8813405 0.8999445 -0.979 0.3296 t 0.1484310 0.0364688 4.070 8.88e-05 *** t2 -0.0003491 0.0003096 -1.128 0.2619 A1 0.9938671 0.4282888 2.321 0.0222 * B1 0.0580218 0.4350546 0.133 0.8941 Adjusted R-squared: 0.5607 Amplituden for 18.6 cyklen er 0.995 cm og modellen giver en forskel i vandstand mellem 1891 og 2005 på 12.1 cm. Når man se på periodogrammet ser det ud til at der også er en variation med en periode på 11 år i dataserien, og da det er velkendt at solen har en 11 års cyklus er det forsøget værd tilpasse en model med denne periode inkluderet. Hvis jeg inkluderer en harmonisk svingning med en periode på 11 år finder jeg: Model 2 coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.9512415 0.8836873 -1.076 0.2841 t 0.1516564 0.0358309 4.233 4.87e-05 *** t2 -0.0003782 0.0003042 -1.243 0.2165 A1 0.9533208 0.4199026 2.270 0.0252 * B1 0.0830706 0.4261882 0.195 0.8458 A2 1.1011287 0.4212893 2.614 0.0102 * B2 -0.0115688 0.4219296 -0.027 0.9782 Adjusted R-squared: 0.5792 A1 og A2 er koefficient for cosinus, B1 og B2 for sinus Amplitude 18.7 år cyklus: 0.95 cm Amplitude 11 år cyklus: 1.1 cm Modellen giver en forskel i vandstand mellem 1891 og 2005 på 10.3 cm. Vedhæftet figur viser "mean_cm" med model i rød og model 2 i grøn. Begge modeller viser at 18.6 cyklussen påvirker tidevandet med 2 cm (2 gange amplituden). I begge modeller er cosinus-termerne og den lineære term statistisk signifikante, men sinus-termerne og den kvadratiske term ikke er det. Det strider i mod din model hvor du skriver at amplituden for 18.6 modellen ikke er statistisk signifikant forskellig fra 0. Min model 1 stemmer heller ikke helt med din model, mon vi kan finde årsagen til det? Jeg har som nævnt fittet de årlige middelværdier af "mean_cm", hvis du har fittet en af de andre kolonner er det måske årsagen. Tilknyttet billede: 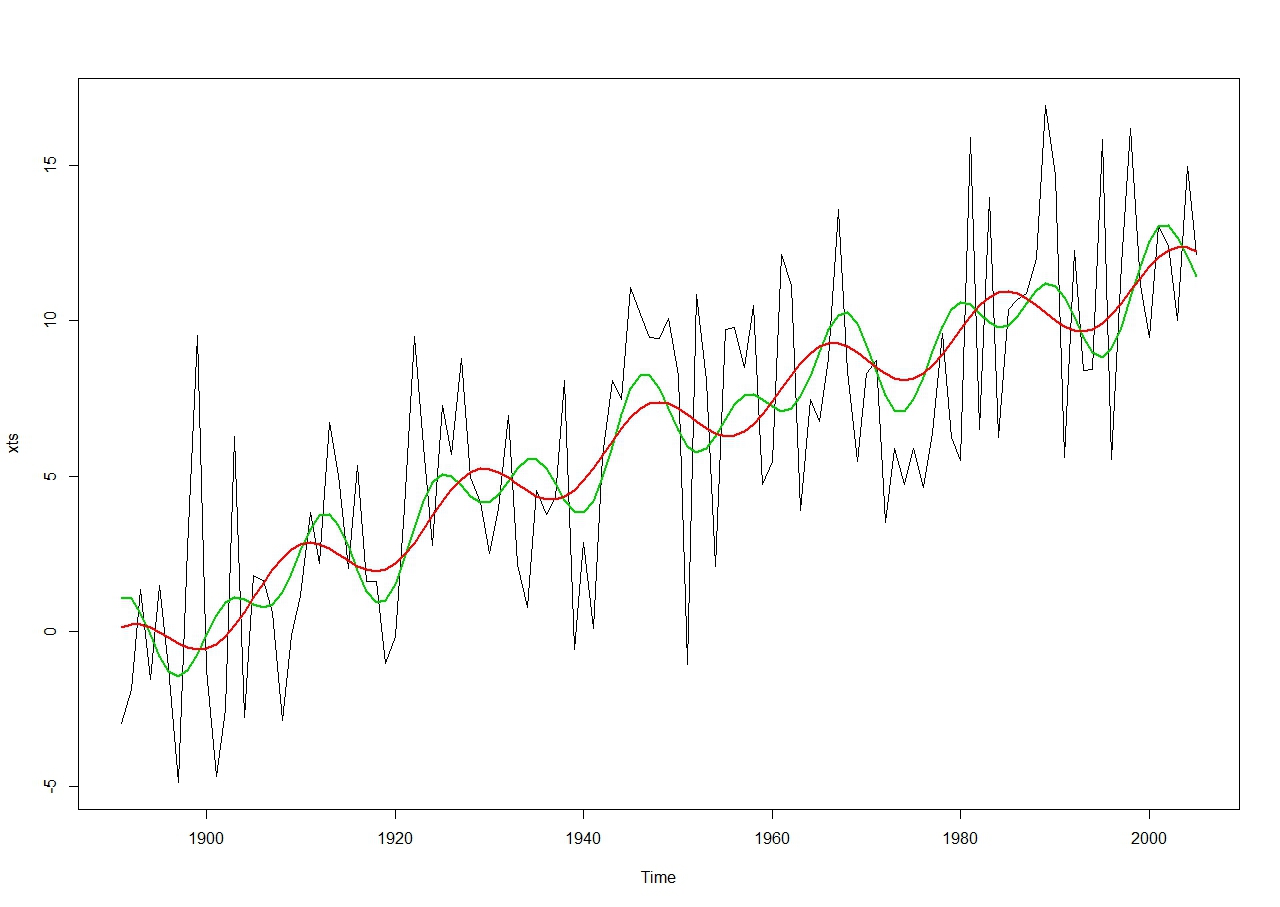
Redigeret d. 18-05-2012 16:32 |
| 18-05-2012 17:58 | |
| kfl★★★★★ (2167) |
Hej SRJ Tak for dit svar. Jeg har lidt problemer med cyklen på 11 år, idet det den ikke er omtalt i de referencer jeg har chekket. Derimod findes der en 8.85 Moon's Perigee cycle. Det gode ved denne diskussion er, at nu sker der en afklaring om spørgsmået i hvertfald 18.6 års-cyklen. Den er konstateret og amplituden kan estimeres for mindst 2 danske stationer. Jeg undersøger videre om der er argumenter for 11 års cyklen eller om man skal se på 8,85 cyklen i stedet for. Det skal også afprøves på tidevandsdata fra Stockholm. Jeg vender tilbage med mere... KFL Vær skeptisk over for skeptikerne.... Det er der grund til. Redigeret d. 18-05-2012 17:59 |
| 19-05-2012 10:56 | |
| kfl★★★★★ (2167) |
Hej SRJ Jeg har arbejdet lidt videre med at søge efter 18.6 års cyklen. Det vil glæde mig, hvis du kan verificere eller falcificere mine resultater. For Gedser og Hornbæk vedkommede er det DMI data jeg anvender , medens det for Stockholms vedkommende er data indsamlet af Martin Ekman og videreformidlet af PSMSL. 18.6 års tidevandscyklen for Gedser, Hornbæk og Stockholm For alle tre stationer har jeg konstateret tilstedeværelse af 18,6 års cyklen både i den årlige middelvandstand og i den månedlige middelvandstand, men med lidt forskellige resultater. Som en tommelfinger regel er amplituden af 18.6 års-cyklen på mellem 0.0 og 1. 5 cm for de indre danske farvande. Der er nogle supplerende analyser og dokumentation, der skal færdiggøres, men mit gæt er at resultatet holder. Gedser tidevandstation(1891-2005): Amplitude af 18,6 års-cyklen: 0,23 cm. Ingen acceleration er konstateret. Ingen 12 eller 6 måneders-cykel. Forskellen mellem den maksimale og minimale daglige vandstand er på ca. 348 cm. Set i denne sammenhæng er 18.6 års-cyklen af mindre betydning. Hornbæk tidevandsstation(1891-2005): Amplitude af 18,6 års-cyklen: 1,21 cm En acceleration er konstateret. Ingen 12 eller 6 måneders cykel. Eksklusiv 2 outliers. Forskellen mellem den maksimale og minimale daglige vandstand er på ca. 312 cm. Set i denne sammenhæng er 18.6 års-cyklen af mindre betydning. Stockholm tidevandsstation (1801-2000) Amplitude af 18,6 årscyklen: 1,38 cm En acceleration er konstateret. Der findes både en 12 eller 6 måneders-cykle i data. Forskel mellem den maximale og minimale månedlige middelvandstand er på 110 cm. De daglige udsving vandstanden er væsentlig større. Set i denne sammenhæng er 18,6 års-cyklen af mindre betydning. Metode: Jeg er startet ud med den fulde model dvs. linear + kvadratisk + cyklerne 18,6 år , 1 år og 0.5 år. Derefter har jeg testet modeller ud indtil jeg har fundet en signifikans. Med forbehold for fejl og mangler og med ret til at opdatere dette indlæg senere i henhold til indkomen kommentarer. KFL Vær skeptisk over for skeptikerne.... Det er der grund til. Redigeret d. 19-05-2012 11:08 |
| 07-05-2013 09:50 | |
| kfl★★★★★ (2167) |
DMI har være så venlige at opdatere tidenvandsdata fra Gedser og Hornbæk til og med 2012. Jeg opdaterer tidevandsanalysen i løbet af 2013. |
| 11-05-2013 21:01 | |
| kfl★★★★★ (2167) |
Nu er DMI kommet på banen mht tilvandsmålinger for Esbjerg, Horbæk og Gedser. DMI Esbjerg Hornbæk Gedser Tak til DMI. Når tids haves, vil jeg ser om jeg når frem til de samme resultater ! Redigeret d. 11-05-2013 21:06 |
| 28-01-2014 17:55 | |
| kfl★★★★★ (2167) |
Jørgen Petersen skrev: Har du stadigvæk synspunktet, at vandstanden har været aftagende i de sidste 10 år ? KFL Vær skeptisk over for skeptikerne.... Det er der grund til. |
| 28-01-2014 18:32 | |
| Kosmos★★★★★ (5371) |
Har du stadigvæk synspunktet, at vandstanden har været aftagende i de sidste 10 år - hmm...du er vel opmærksom på, at JP skrev om (hav)vandstandsSTIGNINGEN?? Redigeret d. 28-01-2014 18:33 |
| 29-01-2014 23:10 | |
| kfl★★★★★ (2167) |
Har du et link ? |
| 30-01-2014 00:30 | |
| Kosmos★★★★★ (5371) |
Har du et link ? - hvem spørger du? Hvis det er mig, står det jo i det citat, du selv indleder med: Ud fra de foreliggende data, er der således ingen tvivl om, at havvandstandsstigningen i de sidste 10 år har været aftagende(min fremhævning). |
| 01-02-2014 21:23 | |
| Jørgen Petersen★★★★★ (4852) |
Tak til Kosmos for et fint svar. Her ud over vil jeg gerne sige, at det er godt nok gamle indlæg, som der her gengives. Det anførte citat er fra den 09.04.2012. Dette indlæg har jeg i mellemtiden glemt alt om. Men indlægget er da af en kvalitet, så det godt kan tåle at blive gengivet. Nu vi er ved at gengive gamle citater, så vil jeg også gerne gengive et af min andre citater fra denne dag: "Uanset Frank Lansner tal eller ej, så ligger havvandsstigningen kun på et meget lavt niveau. Samtidigt er stigningstakten aftagende. Der er således en åbenlys konfligt imellem det diverse alamister med Al Gore i spidsen har meldt ud, og det vi konkret oplever af havvandsstigninger." |
| 07-02-2014 21:37 | |
| kfl★★★★★ (2167) |
Jeg forventer i løbet af de næste par måneder at foretage en opdatering helt frem til 2012 og få rettet diverse fejl og misforståelse samt at få opdateret links. |
Deltag aktivt i debatten Tidevandsmålinger ved Hornbæk og Gedser 1891-2005 version I:
Lignende indhold
| Debatter | Svar | Seneste indlæg |
| Kystdirektoratet 2012, Hornbæk, Gedser, Bodil og returperioder | 20 | 19-10-2023 17:29 |
| Beregning af returperioder for stormfloder ved Hornbæk | 1 | 25-01-2014 10:23 |
| Tidevandsmålinger ved Hornbæk 1891-2005, version I | 10 | 13-12-2013 12:48 |
| Colorado Universitet og satellitmålinger vs. tidevandsmålinger | 0 | 29-05-2012 21:46 |