Sammenligning: Jorden og Venus
| Sammenligning: Jorden og Venus14-04-2020 12:09 | |
| kulden-varmen (2597) |
Hvis lufttrykket er over 92 atm. i et dybt hul i jorden. Hvad ville temperaturen så være? |
| 14-04-2020 15:04 | |
| John Niclasen★★★★★ (6429) |
kulden-varmen skrev: Det er et af de bedste spørgsmål, jeg har set længe. Jeg kan komme med mine bud på svar, men det tager lidt tid at foretage udregningerne, så jeg vender tilbage. Jeg vil have flere lidt forskellige bud, som afhænger af, hvor omfattende beregninger, man udfører. Dvs. hvilke fakta, man skal tage højde for, som at varmekapaciteten af luft ændrer sig med temperatur (og til dels tryk), skal man gå ud fra tør luft, eller skal man regne på en luft indeholdende vanddamp, så varmekapaciteten er en lidt anden, osv. |
| 14-04-2020 20:58 | |
| crank (2455) |
John Niclasen skrev:kulden-varmen skrev: Skidt med det. Når planeten er blevet ubeboelig - kan vi så flytte til Venus? . ☯ |
| 14-04-2020 21:14 | |
| kulden-varmen (2597) |
crank skrev: Ja, vi skal bare ændre lufttrykket på Venus til en atmosfære, så er den næsten beboelig. |
| 14-04-2020 21:29 | |
| crank (2455) |
kulden-varmen skrev:crank skrev: Ja. Det er et stort problem. 8 mia. cykelpumper ville nok bare eksplodere. . ☯ |
| 14-04-2020 23:40 | |
| John Niclasen★★★★★ (6429) |
kulden-varmen skrev: Jeg har foretaget fire forskellige udregninger, som giver lidt forskellige bud på, hvad temperaturen vil være i et hul så dybt, at der er 92 bar tryk nede på bunden her på Jorden. For alle udregninger benytter jeg konstant tyngdeacceleration på 9,82 m/s^2 ned gennem hullet. Dette er tæt på virkeligheden. Tyngdeaccelerationen ændrer sig med afstanden fra Jordens centrum, når man er uden for Jordens radius ud fra formlen: g = GM / R^2 , hvor G er gravitationskonstanten, M er massen af Jorden, og R er afstanden fra Jordens centrum. Når man er inden for Jordens radius, så er det kun massen indenfor ens afstand til Jordens centrum, som skal benyttes. Men samtidig bliver R jo mindre, og det går næsten op de første par tusinde km ned i et hul. Check: Gravity of Earth / Depth 1. Simpel udregning med tør luft og konstant specifik varmekapacitet. Jeg benytter tøradiabaten (Dry Adiabatic Lapse Rate), som fortæller hvor meget temperaturen ændrer sig med højden gennem atmosfæren. Check: Lapse rate Formlen er: - dT/dz = g/c_p , hvor dT er ændringen i temperatur, dz er ændringen i højde, g er tyngdeaccelerationen, og c_p er den specifikke varmekapacitet. Jeg har blot valgt en konstant c_p på 1003,5 J/(kg * K) her i første simple udregning. Varmekapacitet fundet via: http://peacesoftware.de/einigewerte/luft_e.html Check evt. også: https://www.engineeringtoolbox.com/air-specific-heat-capacity-d_705.html For at finde højden, dvs. hvor dybt hullet er, benyttes formlen for hydrostatisk ligevægt: dp/dz = -g rho , hvor dp er ændringen i trykket, dz er ændringen i højden, g er tyngdeaccelerationen, og rho er tætheden. Check: Hydrostatisk ligevægt En formel for tætheden kan udledes ved at antage, at luften opfører sig som en ideal gas, hvilket er en fin antagelse under 'normale' forhold, og så skal man benytte mol-massen, som for tør luft er 28,9654 gram/mol. Jeg vælger trykket ved overfladen til at være 1 atm., altså 1,013 bar, og temperaturen 288 K, som er ca. 15°C. Denne første simple udregning giver, at hullet er 77,457 km dybt, og at der på bunden vil være en temperatur på 1046 Kelvin, hvilket er 773°C. 2. Simpel udregning med fugtig luft og konstant specifik varmekapacitet. Det samme som ovenstående, bortset fra at jeg vælger luft med 1% vanddamp, hvilket giver en lidt anderledes mol-masse og en lidt anderledes specifik varmekapacitet. Resultet er nu, at hullet er 77,467 km dybt, og at der på bunden er 1040 Kelvin, hvilket ca. er 757°C, altså ikke helt så varmt. 3. Avanceret udregning med tør luft og varierende specifik varmekapacitet. Jeg valgte 9 datapunkter for den specifikke varmekapacitet og fittede en ret linie. De 9 punkter var for tryk på 1, 2, 4, 7, 12, 20, 34, 58, og 92 bar og tilhørende temperaturer. Jeg fandt de tilhørende temperaturer ved at køre modellen flere gange med de nye værdier for den specifikke varmekapacitet fundet via ovenstående internet-side. Når man gør det nogle gange, så ændrer værdierne sig næsten ikke længere. Den fittede linie for den specifikke varmekapacitet har hældningen: 0.2113824735481691 og skærer y-aksen ved 934.703744986538 Denne mere korrekte udregning gav, at hullet er 75,646 km dybt, og temperaturen på bunden er 983 Kelvin, hvilket ca. er 710°C. Endnu engang ikke helt så varmt som de første simple beregninger, men stadig varmere end på Venus. Vedhæftede grafer viser de beregnede profiler for tryk og temperatur, jeg har dannet ud fra denne mere avancerede beregning. 4. Simpel udregning med standard lapse rate. Lapse raten på Jorden er ikke den samme overalt. Man har defineret en standard atmosfære for Jorden, som har en lapse rate på 6,49 K/km, eller 6,49°C/km. Hvis man siger, hullet bliver 75,646 km dybt, for at der er 92 bar nede på bunden, og regner med denne mindre lapse rate, så kommer man frem til, at der nede på bunden af hullet er 779 Kelvin, hvilket ca. er 506°C. Der er 737 Kelvin, hvilket ca. er 464°C nede ved den faste overflade på Venus. Check: Venus Fact Sheet @ NASA ---- Tak for spørgsmålet! Jeg vil spørge alle klimaforskere, jeg møder på min vej, om det samme. Tilknyttet billede: 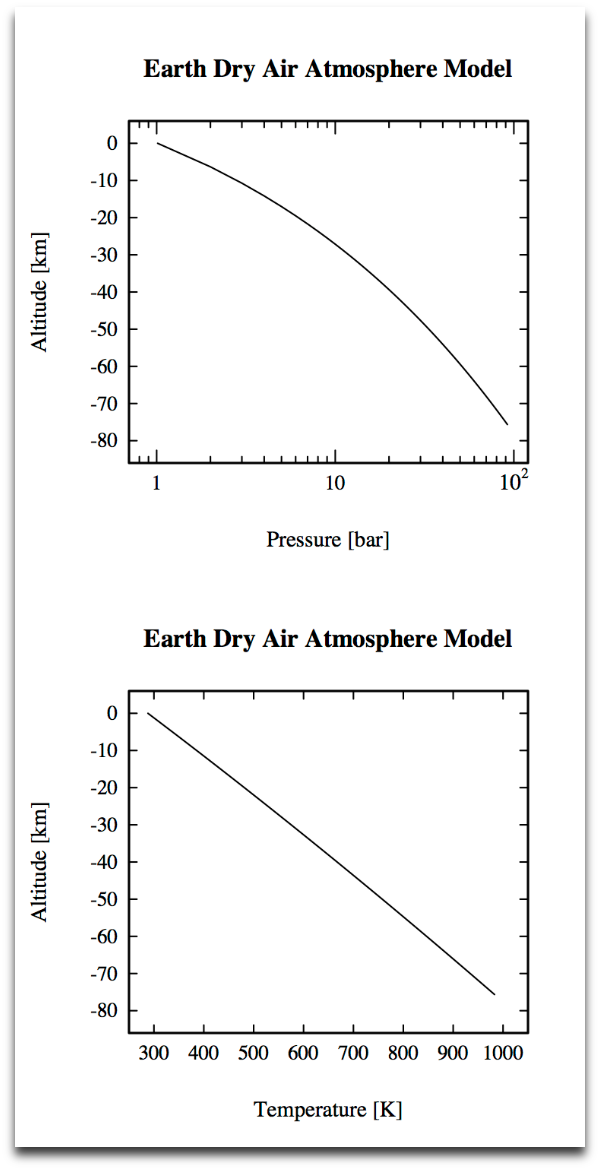 |
Deltag aktivt i debatten Sammenligning: Jorden og Venus:
Lignende indhold
| Debatter | Svar | Seneste indlæg |
| Hvad fortæller Venus os om CO2 som drivhusgas på Jorden? IGEN ! | 136 | 27-05-2023 11:02 |
| Hvad fortæller Venus os om CO2 som drivhusgas på Jorden? | 436 | 28-09-2016 22:29 |
| Klimaet på Venus og Jorden | 437 | 04-09-2016 13:34 |
| Venus - igen igen | 7 | 19-07-2013 22:11 |
| Artikler |
| Ib Lundgaard Rasmussen: Klimaet på Venus - en løbsk drivhuseffekt? |