Peter Laut: Solens aktivitet og Jordens klima
Solens aktivitet og Jordens klima: En re-analyse af nogle tvivlsomme korrelationer
Af Peter Laut, Institut for Fysik, Danmarks Tekniske Universitet
1. BAGGRUND
Inden for det sidste årti er der offentliggjort en række videnskabelige artikler der hævder at have påvist stærke korrelationer mellem forskellige indikatorer for solaktiviteten og nogle parametre for Jordens klima: Det er således blevet hævdet at der skulle eksistere en fin overensstemmelse mellem galaktiske kosmiske strålers intensitet og jordens skydække, først gældende for det totale skydække og derefter ændret til alene at gælde lave skyer, og en fin overensstemmelse mellem solcykluslængder og overfladetemperaturen over land på den Nordlige Halvkugle. Disse korrelationer spiller en betydelig rolle i såvel den videnskabelige litteratur som i den offentlige debat vedrørende risikoen for en menneskeskabt klimaændring. Jeg har analyseret en række af artiklernes centrale grafer. Disse skulle dokumentere de stærke korrelationer, og flere af dem har spillet en væsentlig rolle i klimadebatten og er blevet taget til indtægt for den opfattelse at den observerede globale opvarmning i overvejende grad skyldes Solen. Mine analyser viser imidlertid at de tilsyneladende stærke korrelationer som graferne viser er opnået ved en ukorrekt håndtering af de fysiske data. Jeg mener derfor at graferne ikke kan anvendes som grundlag for konklusioner mht. spørgsmålet om hvorvidt menneskeheden bør eller ikke bør mindske udslippene af drivhusgasser.
Jeg vil gerne understrege at mine analyser ikke på nogen måde udelukker at der eksisterer sammenhænge mellem Solens aktivitet og klimaet på Jorden. Sådanne forbindelser er i årenes løb blevet påvist af mange forskere. Men en signifikant sammenhæng mellem Solens aktivitet og de sidste 140 års globale opvarmning er endnu hverken blevet påvist eller sandsynliggjort. Mit formål med nærværende analyse er således ikke at bevise at Solens aktivitet ikke påvirker eller har påvirket Jordens klima, men blot at gøre opmærksom på at nogle af de figurer der vises igen og igen i videnskabelige artikler, avisindlæg, skolebøger og tv-udsendelser, slet ikke stemmer overens med de fysiske observationer.
Det er følgende artikler jeg har koncentreret mig om:
I det følgende vil jeg diskutere artiklerne i en rækkefølge der afspejler deres grad af aktuel almen interesse.
Ved diskussionen af de publicerede grafer har jeg her valgt at anvende “rekonstruktioner” af de originale figurer, dvs. at jeg har scannet og digitaliseret figurerne elektronisk og derefter plottet de aflæste værdier. Denne fremgangsmåde muliggør en enkel og nøjagtig sammenligning af talværdierne samt giver mulighed for at plotte dem i forskellige formater og farver med henblik på at lette struktureringen og diskussionen af graferne. I visse tilfælde er layoutet imidlertid valgt på en sådan måde at graferne, for alle praktiske formål, er identiske med originalerne.
2. NOGLE SOLHYPOTESER
2.1 “Det totale skydække korrelerer stærkt med intensiteten af galaktisk kosmisk stråling
I året 1997 offentliggjorde Svensmark og Friis-Christensen en artikel hvori de mente at have påvist en stærk korrelation mellem det totale skydække og intensiteten af galaktisk kosmisk stråling som målt ved Climax, Colorado. Denne artikel blev opdateret af Svensmark i 1998. Artiklernes hovedresultat er illustreret ved sidstnævnte artikels Fig. 1. Nedenstående Fig. 1.a er en rekonstruktion af den oprindelige graf opnået som beskrevet ovenfor. Hvis der skulle være opstået mindre afvigelser fra originalen skyldes det at denne er noget utydelig: Nogle områder på originalen er dækket af så megen tryksværte at det er umuligt at aflæse hvilke datasymboler der er afsat. Denne usikkerhed skyldes det store format der er valgt til symbolerne. Eksempelvis er det ikke muligt at afgøre om dataene fra Defense Meteorological Satellite Program (DMSP)1 - som repræsenteres ved romber - i årene 1990-92 følger den ‘hængekøjefacon’ som den kosmiske stråling angiver, eller om de i det mindste følger den nedadgående tendens som både den kosmiske stråling og ISCCP-dataene2 følger. Disse spørgsmål er naturligvis vigtige hvis man vil finde ud af om DMSP-dataene overhovedet hører hjemme på denne graf, om de overhovedet repræsenterer totalt skydække, dvs. den samme fysiske størrelse som ISCCP-dataene. På figuren kan der tydeligt skelnes romber fra 1988-90 og fra 1992- 1995, men den originale figur fra Svensmark (1998) tillader ikke at afgøre om de også bidrager til det stærkt sværtede område i perioden 1990-92. Her kommer heldigvis nogle analyser til hjælp der er foretaget af de to norske forskere Kristjánsson og Kristiansen (2000). De gør det muligt at fastslå at DMSP-dataene i virkeligheden har et forløb der hverken stemmer overens med ‘det totale skydække’ eller med kosmisk stråling.
Bemærk i øvrigt at Svensmarks figur for det meste af år 1992 synes at indikere at det totale skydække på en og samme tid skulle have været usædvanligt beskedent (iflg. den lave kurve) og usædvanligt kraftigt (iflg. den høje kurve).
Fig. 1.b viser en sammenligning af DMSP-dataene med ISCCP’s data for totalt skydække som præsenteret i Kristjánsson og Kristiansen (2000). Fig. 1.b er en rekonstruktion af deres originale figur, idet deres data her er vist i samme layout som Svensmarks figur for at muliggøre en direkte sammenligning. Figuren viser at de to dataserier, DMSP og ISCCP, forløber helt forskelligt. I de tidsintervaller hvor de overlapper aftager det totale skydække iflg. ISCCP samtidigt med at DMSP-værdierne vokser. Det samme gælder de to seriers samlede trend. Hvis man derfor antager at ISCCP-serien giver et korrekt billede af det totale skydækkes udvikling i tiden, kan DMSP-dataene umuligt også repræsentere totalt skydække.
Fig. 1.c er en korrigeret og ajourført version af Svensmarks originale figur (her reproduceret som Fig. 1.a). Korrektionen består i fjernelsen af DMSP-dataene, der jo er irrelevante her da de ikke repræsenterer totalt skydække. Ajourføringen består i en tilføjelse af nyere data for totalt skydække fra http://isccp.giss.nasa.gov/climanal1.html (ISCCP D2 data for perioden 1983-99, udglattet med en båndbredde svarende til Fig. 1.a). Derudover viser figuren også den kosmiske stråling (GCRI) som målt ved Climax i Colorado. Figuren viser at det totale skydække stemmer ganske fint overens med den kosmiske stråling i perioden 1985-89 hvorefter kurverne går hver sin vej: det totale skydække falder kraftigt i de efterfølgende år mens intensiteten af den kosmiske stråling stiger kraftigt.
Analyserne i Kristjánsson og Kristiansen (2000) viser at perioden med overensstemmelse (1985-89) blev udvidet kunstigt på Fig. 1.a ved at kombinere to dataserier der repræsenterer to forskellige fysiske størrelser (ISCCP og DMSP) på en sådan måde at de giver indtryk af at danne en enkelt sammenhængende kurve. Der er altså tale om det der på jævnt dansk kaldes “at blande æbler og pærer”. Fig. 1.a har spillet en vigtig rolle både i den videnskabelige litteratur og i den offentlige debat om de mulige årsager til den globale opvarmning.
2.2 “Lavt skydække korrelerer stærkt med intensiteten af galaktisk kosmisk stråling
” I året 2000 præsenterede Marsh og Svensmark (2000) en ny hypotese der gik ud på at det var ‘dækket af lave skyer’ (og altså ikke det ‘totale skydække’ som hævdet i Svensmark 1998), der korrelerede stærkt med den kosmiske stråling, som i deres artikel var repræsenteret ved data fra den peruvianske observations-station Huancayo. Den centrale graf (Fig. 1.c) i deres artikel er i nærværende artikel gengivet som Fig. 2.a (igen en rekonstruktion). Fig. 2.b viser en opdatering ved Kristjánsson et al. (2002) og Fig. 2.c en udglattet version af sidstnævnte kurve. En sammenligning med Fig. 2.a giver anledning til en række kommentarer:
(1) Overensstemmelsen mellem det lave skydække og kosmisk stråling er ikke god efter år 1989, og efter år 1994 er der absolut ingen overensstemmelse.
(2) Ved første øjekast synes den stejle stigning af det lave skydække efterår 1992 (se fx Fig. 2.c) at svare ganske godt til en tilsvarende stigning i den kosmiske stråling. Imidlertid er stigningen i det lave skydække mere end et halvt år forsinket i forhold til den kosmiske stråling. Ifølge gældende teori (fx Yu og Turco 2000) skulle den udvikling af kondensationskerner for skydannelsen, der har ionerne fra den kosmiske stråling som kim, være tilendebragt mindre end et døgn efter at en stigning i den kosmiske stråling har fundet sted. Og da levetiden af sådanne aerosoler (kondensationskerner) kun beløber sig til nogle få dage må en evt. skydannelse finde sted inden for denne tidshorisont og ikke flere måneder senere. En skydannelse der sker som respons på ændringer i kosmisk stråling, må derfor fremtræde som praktisk taget samtidigt med ændringerne i den kosmiske stråling når den afbildes i den tidsskala der anvendes på Fig. 2.
(3) En anden vanskelighed er den fysiske tolkning af infrarød data fra satellitobservationer til bestemmelse af det lave skydække: Lave skyer der befinder sig neden under højere skyer kan ofte slet ikke observeres fra satellitter, og da den relative variation af de forskellige skytyper kun andrager nogle få procent kan selv en beskeden fejl ved bestemmelsen af det lave skydække påvirke kurveforløbet på en væsentlig og samtidig tilfældig måde, således at sammenligninger med andre kurver bliver meningsløse.
Kernthaler et al. (1999) har studeret forskellige typer skyer og har ikke fundet nogen overensstemmelse mellem de enkelte skytyper og kosmisk stråling. Wagner et al. (2001) har sammenlignet en ‘proxy’ for kosmisk stråling, nemlig koncentrationer af isotoperne 10Be og 36Cl, med ‘proxy’er’ for Jordens klima, 018O- og CH4-koncentrationen, over tidsperioden fra 20.000 til 60.000 år før nu og ikke fundet nogen korrelation. Kristjánsson et al. (2002) har sammenlignet korrelationen af det lave skydække med hhv. solarkonstanten (= total solar irradiance) og GCRI og fundet at korrelationskoefficienten med total solar irradiance er langt den største (r = 0.80 mod r = 0.47). Dette resultat kunne pege i retning af at solaktiviteten måske virkeligt påvirker udstrækningen af det lave skydække, men at den fysiske mekanisme i virkeligheden er knyttet til ændringer i Solens elektromagnetiske udstråling, og ikke til kosmisk stråling. Det ville stemme godt overens med en mekanisme der har været diskuteret i de senere år (Bond et al. 2001, Haigh 2001, Shindell et 1999, 2001) hvor det antages at temperaturændringer i stratosfæren, forårsaget af ændringer i Solens ultraviolette bølgelængder (ændringer som relativt er betydeligt større end ændringerne i det synlige område), giver anledning til en dynamisk respons i troposfæren som måske kan påvirke Jordens klima. Muligvis spiller planetariske bølger en vigtig rolle ved disse processer. Derfor kan den delvise overensstemmelse mellem det lave skydække og GCRI som vises i Marsh og Svensmark (2000) skyldes den omstændighed at GCRI og solarkonstanten begge er fysiske størrelser der er knyttet til solaktivitet, og at en årsagssammenhæng mellem det lave skydække og solarkonstanten automatisk vil medføre en vis, men mindre grad af overensstemmelse med GCRI, selv i det tilfælde hvor kosmisk stråling ikke spiller nogen rolle ved de fysiske processer der fører til dannelsen af lave skyer.
En alternativ forklaring af den dårlige overensstemmelse mellem GCR og det lave skydække efter 1994 (som vist på Fig. 2.b and Fig. 2.c) er fremsat af Marsh og Svensmark (2002), der hævder at den manglende overensstemmelse er et artefakt der skyldes problemer med instrumentkalibreringen mellem september 1994 og januar 1995. En diskussion af mulige forklaringer og mulige fysiske processer er givet af Carslaw et al. (2002).
Da variationen af den ultraviolette udstråling fra solen over de sidste 100 år ikke er kendt, og da mekanismerne for dens mulige klimapåvirkning ikke er afklaret, ikke mindst graden af nonlinearitet, er det endnu ikke muligt at afgøre hvorvidt disse processer har bidraget til den globale opvarmning som Jorden har oplevet over denne periode.
2.3 “Solcykluslængder korrelerer kraftigt med overfladetemperaturen over land på den Nordlige Halvkugle (1991)”
I 1991 offentliggjorde Friis-Christensen og Lassen i det ansete videnskabelige tidsskrift Science en artikel hvori de mente at have påvist en “slående god overensstemmelse” mellem solcykluslængder (SCL) og lufttemperaturen ved overfladen over den Nordlige Halvkugles landområder. Artiklen vakte stor opmærksomhed over hele verden og bliver stadigvæk ofte citeret i den videnskabelige litteratur. En søgning i Science Citation Index Expanded fra Institute for Scientific Information viser at artiklen er blevet citeret 213 gange fra 1991 til september 2002. I den senere tid er den blevet citeret en eller to gange om måneden. Også i den offentlige debat om de mulige årsager til den globale opvarmning spiller den stadigvæk en stor rolle (se fx DER SPIEGEL 2001). Artiklens centrale figur (Fig. 2 i Science-artiklen; fx gengivet i Vejret nr. 1, 1992) er i nærværende artikel vist som Fig. 3.a der igen er en rekonstruktion - her med tilføjelse af en nummerering (fra 0 - 4) af nogle kurvepunkter for at lette struktureringen og diskussionen. Af særlig interesse er den meget fine overensstemmelse mellem de seneste årtiers kraftige globale opvarmning og den tilsvarende stejle stigning i solcykluskurven. Den offentlige debat har netop fokuseret på de seneste årtiers markante globale opvarmning, og den tilsyneladende overensstemmelse mellem temperaturkurven og solkurven har overbevist mange mennesker om at det er solen, og ikke menneskeskabte drivhusgasser, der har været årsagen til denne opvarmning.
En omhyggelig analyse afslører imidlertid nogle problematiske detaljer: Figurens solcykluskurve består af i alt 24 punkter. Heraf er de første 20 punkter “1,2,2,2,1- filtrerede” værdier, dvs. at de er beregnet som løbende gennemsnit over fem på hinanden følgende observerede maksimum-maksimum eller minimum-minimum solcykluslængder med vægtfaktorerne: 1/8, 2/8, 2/8, 2/8, 1/8. Hvert af disse 20 punkter repræsenterer altså observationer over et tidsinterval på omkring 55 år (5 gange den gennemsnitlige solcykluslængde på 11 år). Det betyder at for hvert punkt der afsættes kræves der et kendskab til udviklingen af solpletantallet ca. 28 år ud i fremtiden og 28 år bagud i tiden. Kurvens første 20 punkter er altså fremkommet som resultat af en meget kraftig udglatning (eller ‘filtrering’) af de observerede data. Sammenligner man denne udglattede kurve med de ikke-filtrerede solcykluslængder, dvs. med de observerede data, finder man at de ikke-filtrerede værdier udfører voldsomme svingninger op over og ned under den udglattede kurve. Punkterne nr. 3 og 4 på Fig. 3.a repræsenterer sådanne ikke-filtrerede solcykluslængder, medens punkterne nr. 1 og 2 repræsenterer data som kun er delvist filtreret. Den tilsyneladende overensstemmelse mellem solkurven og temperaturkurven er opnået kunstigt ved at kombinere den udglattede kurves 20 punkter med det seneste opsving i den række af kraftige udsving op og ned som de observerede solcykluslængder udviser, dvs. ved at kombinere forskelligartede fysiske datasæt, eller sagt på jævnt dansk: ved at ‘blande æbler og pærer’. Hvis man i stedet for havde kombineret den udglattede kurve med et udsving nedad ville solcykluskurven i stedet have stemt fint overens med en dramatisk global afkøling. Denne kombination kunne man så have valgt hvis en sådan global afkøling havde fundet sted (Problemet diskuteres detaljeret i Laut og Gundermann 2000). Dette demonstrerer at det kan give misvisende resultater at blande forskellige typer data på denne måde. For at undgå en sådan sammenblanding burde de sidste fire punkter have været udeladt i den oprindelige publikation. Herved var solcykluskurven kommet til at se ud som vist på Fig. 3.b, hvor den ender i punkt nr. ‘0': Dette punkt markerer den sidste solcyklusværdi der på tidspunktet for artiklens offentliggørelse i 1991 kunne beregnes korrekt, dvs. ved en 1,2,2,2,1-filtrering.
I dag, hvor der i mellemtiden er kommet flere observationer, kan kurven forlænges ud over punkt ‘0'. Fig. 3.c viser den opdaterede solcykluskurve med de nye (1,2,2,2,1-filtrerede) punkter nr. 1 - 4 tilføjet. Lassen og Friis-Christensen (2000) og Thejll og Lassen (2000) præsenterer også opdaterede værdier for disse fire punkter, men ved nærmere eftersyn viser det sig at opdateringerne til dels er præget af regnefejl. Begge artikler anvender dels de to solcykluslængder der i mellemtiden har kunnet måles og dels forudberegnede værdier for tidspunkterne for det næste solpletminimum og det næste solpletmaksimum. Begge artikler benytter nøjagtigt de samme data, og disse er også anvendt til beregning af Fig. 3.d (se Tabel 1 nedenfor). Thejll og Lassen (2000) præsenterer deres opdaterede værdier såvel i deres Fig. 1 og i Fig. 2. Fig. 3.c viser hvordan solcykluskurven med deres fejlbehæftede opdatering kommer til at se ud. Det er punkterne 3 og 4 der er behæftede med simple numeriske regnefejl, og det er alene takket være disse regnefejl at kurven opnår den stejle stigning som passer så fint med de sidste årtiers globale opvarmning. Man kan overbevise sig selv om regnefejlen ved simpelthen at regne efter. De 1,2,2,2,1-vægtede gennemsnit af de SCL-værdier som forfatterne benytter er vist i søjle 4 på Tabel 1: 1/8*10.6 +2/8*11.6 +2/8*10.3 +2/8*10.0 +1/8*10.5 = 10.61 og 1/8*11.0 +2/8*11.0 +2/8*9.7 +2/8*10.7 +1/8*10.9 = 10.59. Så det må konkluderes at den “stejle stigning” der vakte så stor opmærksomhed i 1991, hverken understøttes af de data der var tilgængelige i 1991 eller af de data der siden hen er fremkommet. Lassen og Friis-Christensen (2000) angiver de samme forkerte værdier (= 10.6, 10.6, 10.5, 10.1 år) som Thejll og Lassen (2000) for de opdaterede 1,2,2,2,1- filtrerede SCL’er og henleder tilmed særlig opmærksomheden på den ‘stejle stigning’ som de fejlbehæftede punkter 3 og 4 giver solcykluskurven og som umiddelbart synes at retfærdiggøre deres oprindelige beskrivelse i 1991-artiklen af en “slående god overensstemmelse” og “en tæt forbindelse mellem de to kurver i de opadgående trends fra 1900 til 1940 og siden 1970", dvs., over de sidste årtiers globale opvarmning. Tabel 1 samler de data der kræves for at læseren selv kan studere problemet lidt nærmere.
En graf der ofte optræder i den seneste tids klimadebat, er Fig. 3 i Thejll og Lassen (2000). Nedenstående Fig. 4 viser de to centrale kurver fra denne figur (dvs. temperaturkurven og de 1,2,1-filtrerede solcykluslængder) sammen med de 1,2,2,2,1-filtrerede solcykluslængder fra Fig. 2 i Friis-Christensen og Lassen (1991) suppleret med den ovennævnte (korrekte) opdatering af punkterne 1-4. Det ses at forfatterne, ved at forlade den oprindelige hypotese (der involverede de 1,2,2,2,1-filtrerede data) til fordel for en 1,2,1-filtrering, har opnået en noget bedre overensstemmelse med temperaturudviklingen - et eksempel på den generelle erfaring at kurvetilpasninger ofte kan forbedres ved at skifte udglatningsmetode efterhånden som nye observationer bliver tilgængelige.
Når man undersøger mulige korrelationer mellem to tidsserier er det altid klogt at anvende et tidsinterval der er så bredt som muligt. På Fig. 5 sammenlignes de 1,2,2,2,1- filtrerede minimum-minimum solcykluslængder med udglattede temperaturer på den Nordlige Halvkugle dækkende perioden fra 1400-1990. Temperaturserien er fremkommet ved at kombinere den rekonstruerede temperaturserie af Mann et al. [1998] med den moderne, termometerbaserede serie fra Hadley Centret (Combined land air and sea surface temperature anomalies for the Northern Hemisphere 1951-1998, på http://www.meto.gov.uk/ sec5/ CR_div/ Tempertr/ lsst_ vals _nh.html). SCL-værdierne på Fig. 5 kan findes i Tabel 1 i Lassen og Friis-Christensen (1995). SCL-data fra år 1610 til nu kan hentes på web-adressen: ftp://ftp.ngdc.noaa.gov/STP/SOLAR_DATA/SUNSPOT_NUMBERS/maxmin.new. Parametrene er i det væsentlige de samme som dem der er vist på Fig. 3.a, men dækker her en længere tidsperiode. Tilpasningen af solkurven til temperaturkurven er opnået ved lineær regression. Det ses at den lineære regression giver en langt dårligere overensstemmelse mellem solcykluskurven og den terrestriske temperaturkurve når man som her prøver at få kurverne til at stemme overens over en lang tidsperiode, hvor de hver for sig opviser mange specifikke karakteristika. Her er sandsynligheden for at opnå en god overensstemmelse ringe - medmindre der virkelig eksisterer en årsagssammenhæng. Den ramme der er indtegnet på Fig. 5 angiver variabelintervallerne på Fig. 3.a, dvs. den oprindelige figur i Friis-Christensen og Lassen (1991). Hvis man prøver at skalere de to kurvers ‘S-former’ inden for rammen således at tilpasningen bliver optimal (som det rent faktisk er gjort på Fig. 3.a), kræver det en skaleringsfaktor der samtidigt med den gode tilpasning inden for rammen giver en dårlig tilpasning uden for. Eksempelvis ville uoverensstemmelsen mellem solkurven og temperaturkurven omkring år 1600, hvor den ene har en ‘top’ samtidig med at den anden har en ‘dal’, blive forstærket kraftigt. Omvendt: Hvis man valgte at optimere kurvetilpasningen i et tidsinterval omkring 1600 så ville skaleringsfaktoren simpelthen skifte fortegn og derved omdanne ‘toppen’ på solkurven til en ‘dal’ som ville stemme fint overens med ‘dalen’ på temperaturkurven. Men nu ville overensstemmelsen mellem kurverne uden for det nye interval (bl.a. i det indrammede interval) blive dårlig.
Det skal lige bemærkes at Fig. 5 her kun tjener til kvalitativt at illustrere et generelt træk ved lineære regressioner. Derfor er det uden betydning at de to temperaturserier der her er sammenføjet har forskellige referenceperioder og at dette i nærværende sammenhæng kun er søgt kompenseret ved en simpel additiv nulpunktskorrektion.
2.4 “Solcykluslængder korrelerer stærkt med overfladetemperaturen over land på den Nordlige Halvkugle (1995)”
I 1995 offentliggjorde Lassen og Friis-Christensen en ajourført og udvidet udgave af deres Science-artikel fra 1991. Dens centrale figur (Fig. 2 i deres artikel) vises nedenfor som Fig. 6.a (som rekonstruktion). Kurven med cirklerne viser solcykluslængder. De to optrukne kurver viser to forskellige temperaturserier. Den originale figur kan let give det indtryk at der kun er tale om en enkelt temperaturkurve der strækker sig over hele intervallet. I virkeligheden er temperaturudviklingen dog repræsenteret ved to forskellige serier: En serie der spænder fra 1585-1866 og en anden der spænder fra 1862-1982, med et overlap fra 1862-66. De to kurver er på Fig. 7 vist (også optrukket ) i lidt større format. Her ses det tydeligt at der er tale om to forskellige serier der overlapper, og som i det tidsrum hvor de overlapper, er parallelforskudt i forhold til hinanden svarende til en lodret afstand på omkring 0.1 ºC. Denne ejendommelige forskydning skyldes at forfatterne har afbildet de to serier direkte som rå temperaturanomalier, dvs. uden at tage i betragtning at de er målt i forhold til to forskellige referenceperioder. Dette forhold er blevet diskuteret i detaljer af Laut og Gundermann (1998). De ældre temperaturer på Fig. 6.a stammer fra Groveman og Landsberg (1979a, 1979b, 1979c) som i 1979 offentliggjorde en temperaturrekonstruktion for perioden 1579-1880. Som referenceperiode valgte Groveman og Landsberg intervallet 1881-1975, idet de byggede på en temperaturserie der var offentliggjort af Borzenkova et al. (1976). Ved at kombinere deres egen rekonstruerede serie med Borzenkovas data kunne Groveman og Landsberg opstille en serie af anomalier der spændte fra 1579-1975. Denne serie er vist som Fig. 1 i Groveman og Landsberg (1979a). Figur 7 nedenfor viser et løbende 11-årsgennemsnit af denne Groveman / Landsberg / Borzenkova temperaturserie (den punkterede linje). Serien kunne have været anvendt umiddelbart af Lassen og Friis-Christensen (1995) i deres sammenligning mellem solcykluslængder og overfladetemperaturen, idet den dækker hele det tidsinterval for hvilket der forelå solcykluslængder. Men i stedet for at anvende disse indbyrdes konsistente data brugte Lassen og Friis-Christensen (1995) en kombination af to forskellige temperaturserier med hver sin referenceperiode og derfor også med hver sin temperaturskala:
(1) Serien fra 1585-1866 på deres graf er en noget forenklet udgave af et 11-års løbende gennemsnit af Groveman / Landsbergs rekonstruktion. Den er vist som den venstre temperaturkurve såvel på Fig. 6.a som på Fig. 7. Serien er - ejendommeligt nok - ikke et korrekt 11-års løbende gennemsnit sådan som forfatterne beskriver den i deres artikel. Som det ses på Fig. 7 afviger den fra det korrekte 11-års løbende gennemsnit derved at en del af oscillationerne er fjernet. Den nøjagtige karakter af disse beskæringer er uklar.
(2) De nyere temperaturer på Fig. 6.a (dvs. den højre temperaturkurve på Fig. 6.a og Fig. 7) stammer fra Jones et al. (1986), Jones (1988) og Jones et al. (1998) som er defineret med 1951-70 som referenceperiode. Denne kurve er meget lig Groveman / Landsberg / Borzenkova-serien, bortset fra den ovennævnte forskydning nedad på omkring 0.1 ºC. Forskydningen skyldes den omstændighed at gennemsnitstemperaturen for Jones-seriens referenceperiode (1951-1970) lå omkring 0.1oC højere end gennemsnitstemperaturen for den referenceperiode (1881-1975) som definerer Groveman / Landsberg / Borzenkovaserien. Det betyder at talværdierne for Jones’ data kommer til at ligge omkring 0.1 ºC lavere end for de tilsvarende Borzenkova-data, selv om de to seriers temperaturforløb - når de udtrykkes i samme skala - stort set er identiske. Den forskydning nedad af den højre temperaturkurve (med de nyere temperaturer) får rundt regnet en tredjedel af den globale opvarmning der er sket over det tidsinterval som grafen dækker, til at forsvinde. Derved forbedres temperaturkurvens overensstemmelse med solcykluskurven. Kombinationen af disse to temperaturserier udtrykt i forskellige temperaturskalaer skaber således et forkert indtryk af overensstemmelse mellem solaktivitet og temperaturen på Jorden ved tilsyneladende at mindske den observerede globale opvarmning.
En anden ejendommelighed der bidrager til den tilsyneladende gode overensstemmelse på Fig. 6.a mellem solcykluskurven og den globale opvarmning er at solcykluskurven er blevet ‘løftet’ i hele dens udstrækning således at den passer meget fint med de (sænkede) moderne Jones’-temperaturer. Den forbedrede overensstemmelse mellem kurverne på figurens højre side er imidlertid opnået på bekostning af overensstemmelsen på figurens venstre side. Her ses det at næsten alle solcykluspunkter svæver højt over temperaturkurven. Var der blevet anvendt en simpel lineær regression ville antallet af solcyklusværdier over og under temperaturkurven stort set have været det samme. Kurvetilpasningen er altså her foretaget manuelt hvorved der er fremkommet en god overensstemmelse i netop den tidsperiode hvor bidrag fra menneskeskabte drivhusgasser er mistænkt for at have spillet en væsentlig rolle.
Fig. 6.b viser en korrigeret udgave af Fig. 6.a hvor visse ændringer i databehandlingen er indført: (1) I stedet for at anvende to forskellige temperaturserier med talværdier angivet i hver sin temperaturskala anvendes Groveman / Landsberg / Borzenkova-serien i sin helhed. Her er alle data angivet i samme temperaturskala. (2) Tilpasningen mellem solcykluskurven og temperaturkurven er her opnået ved simpel lineær regression, dvs. uden efterfølgende manuel tilpasning. (3) For at undgå at en mulig sol/jord-korrelation kunne blive ‘kontamineret’ af en - i denne sammenhæng - uvedkommende faktor, nemlig et eventuelt menneskeskabt bidrag til den globale opvarmning, er kun data før 1850 taget med i den lineære regression. I tilfælde af at det skulle vise sig at data fra før 1850 rummer en betydelig korrelation mellem solcykluslængder og terrestriske temperaturer, ville man så kunne undersøge om overensstemmelsen - med de samme regressionskonstanter - også gjaldt data efter 1850. En god overensstemmelse også efter år 1850 ville da kunne tolkes som et stærkt indicium for at den menneskelige indflydelse måtte være ubetydelig og at temperaturforløbet i det væsentlige er styret af Solens aktivitet og i dag simpelthen følger samme før 1850. Imidlertid følger temperaturkurven, som det ses af Fig. 6.b, ikke solcykluskurven, men stiger umiskendeligt over den.
2.5 “Solcykluslængder korrelerer stærkt med overfladetemperaturerne over land på den Nordlige Halvkugle (2000)”
I forbindelse med en artikel af Laut og Gundermann (2000a) der kritiserede Friis-Christensen og Lassen (1991), offentliggjorde disse forfattere en ‘svar-artikel’ (Lassen og Friis-Christensen 2000). I dette arbejde præsenterede de en ajourført udgave af deres 1995-resultater (vist som Fig. 6.a ovenfor). Den ajourførte udgave (Fig. 2 i deres nye artikel) er vist nedenfor som Fig. 8.a (en rekonstruktion). Det viser sig at det ikke er helt ligetil at gennemføre en kontrolberegning af denne figur da forfatterne kun giver en meget ufuldstændig forklaring på hvordan kurvetilpasningen er opnået. De nævner at de har indført vægtfaktorer på de observerede solcykluslængder der tager højde for at de ældre data er noget usikre. Imidlertid giver de ingen oplysninger om hvilke talværdier de har valgt for disse vægtfaktorer. En detaljeret analyse ved Laut og Gundermann (2000b) viser at forfatterne, for at nå frem til Fig. 2 i deres artikel (Fig. 8.a nedenfor) må have sat samtlige vægtfaktorer for data før år 1800 til nul eller til værdier meget nær ved nul. Fig. 8.b er opnået ved netop at sætte disse vægtfaktorer til nul. Det ses at Fig. 8.b stort set er identisk med Fig. 8.a. Dette valg af vægtfaktoren nul for alle soldata dækkende de første 230 år af solcyklusserien skal kommenteres: Fysiske data der fortjener en vægtfaktor på nul burde slet ikke vises på en graf af nærværende art. De må være alt for usikre til overhovedet at blive taget med i betragtning. Og hvis de af en eller anden grund alligevel tages med, så bør læseren advares imod at tillægge dem nogen værdi.
En anden interessant ændring i den ajourførte Fig. 8.a fra år 2000 i forhold til den originale Fig. 6.a fra år 1995 er det faktum at antallet af de data der dækker perioden 1850- 1980 er blevet fordoblet ved at tilføje 1,2,2,2,1-filtrerede maksimum-maksimum cykluslængder til de minimum-minimum cykluslængder som oprindeligt blev anvendt. Her skal det bemærkes at maksimum-maksimum cykluslængder i mange analyser (det gælder således 1995-artiklen) ikke anvendes fordi de anses for at være mindre nøjagtige. Ved denne fordobling af datapunkter inden for et specifikt interval fordobles også den matematiske vægt hvormed dette interval indgår i den lineære regression. Det medfører en kurvetilpasning der optimerer overensstemmelsen af de to ‘S-formede’ afsnit på hhv. solcykluskurven og temperaturkurven (som også er omtalt ovenfor i forbindelse med Fig. 5) på bekostning af tilpasningen i resten af kurvernes forløb. Da der er en begrundet mistanke om at temperaturerne netop på det ‘S-formede’ afsnit er stærk påvirket af menneskeskabte drivhusgasser, risikerer man at en eventuel korrelation der påvises på denne måde snarere skyldes en tilfældig covarians mellem solaktiviteten og en stigende menneskelig aktivitet (startende med den industrielle revolution) frem for en påvirkning af Jordens klima ved processer på Solen.
Nedenstående Fig. 8.c er baseret på praktisk taget de samme data som Fig. 8.a, idet der dog er foretaget følgende ændringer i databehandlingen: (1) Der er ikke set bort fra de første 230 års solcykluslængder. (2) Antallet af datapunkter mellem 1850 og 1980 er ikke blevet fordoblet. (3) Den lineære regression er blevet indskrænket til at omfatte data fra før 1850 for hvilke en evt. påvirkning fra menneskeskabte drivhusgasser endnu kan anses for at være relativ beskeden. (4) Alle de anvendte data har fået tildelt samme vægtfaktor i den lineære regression.
3. KONKLUSION
Flere af de figurer der diskuteres ovenfor har påkaldt sig stor opmærksomhed verden over, såvel i videnskabelige sammenhænge som i den løbende offentlige diskussion om muligheden af menneskeskabte klimaændringer. Jeg har ovenfor søgt at vise at de er fremkommet ved en ukorrekt databehandling. Da erkendelsen af at de ikke giver et korrekt billede af den fysiske virkelighed, stadigvæk ikke er særlig udbredt har jeg fundet det på sin plads at offentliggøre nærværende kritiske analyse.
Hvad angår den række nyere undersøgelser der tyder på at variationer i sollysets indhold af ultraviolet stråling måske påvirker Jordens klima ved at modulere temperaturen i stratosfæren og derved påvirke luftcirkulationen i troposfæren (Bond et al. 2001, Haigh 1996, 2001, Shindell et 1999, 2001) så er det meget vel muligt at man her er ved at have identificeret nogle afgørende fysiske klimamekanismer for sol-jordvekselvirkningen. Imidlertid er yderligere analyser nødvendige for at belyse og bekræfte deres rolle.
Til sidst vil jeg gerne give udtryk for at jeg - frem for den ovenfor leverede kritik - langt hellere ville have præsenteret en positiv gennemgang af forfatternes hypoteser og resultater. Ikke mindst af personlige hensyn til alle parter. Men jeg vil også understrege at jeg anser korrektioner til videnskabelige artikler som en forpligtelse vi forskere har - både over for hinanden og over for resten af samfundet. Vi er - efter min mening - ikke blot forpligtet t il selv at levere sandfærdig information, men også til at gøre opmærksom på det, når videnskabelige artikler på væsentlige områder leverer misinformation.
NOTER
1 DMSP står for “Defence Meteorological Satellite Project”. Målingerne foretages med “Special Sensor Microwave/Imager (SSM/I)”. Der måles bl.a. hyppigheder af skyforekomster over oceanerne, og der registreres kun ‘vandskyer’, dvs. skyer der består af vanddråber. Den betydelige andel af skyer der indeholder iskrystaller detekteres altså ikke. Dens tolkningen af de målte mikrobølgedata er ikke verificeret ved sammenligning med synoptiske data (observationer med øjet). DMSP-dataene afviger dramatisk fra og ISCCP-data, selv om man sammenligninger DMSP-serien med ISCCP-data for skyer der kun består af vanddråber. Årsagen til afvigelsen er ikke forstået (se Kristiánsson og Kristiansen 2000). Mulige forklaringer er at sensorerne ikke kan skelne vandskyerne fra andre fænomener og instrumentdrift.
2 ISCCP står for “International Satellite Cloud Climatology Project” . Der foretages målinger af elektromagnetisk stråling i det infrarøde og synlige område. Måleinstrumenterne er anbragt om bord på geostationære og polare meteorologiske satellitter. Herved produceres der datasæt for det globale skydække og for skyernes fysiske egenskaber. Tolkningen af disse data er verificeret med synoptiske data. Projektet har publiceret forskellige dataserier med forskellig struktur. Serienummeret indgår i navnet. De serier der er benyttet på Fig. 1.a-c hedder således ISCCP C2 og ISCCP D2. Målingerne fra dette ISCCP anses generelt for at være de bedste data der eksisterer på området. Datasættet er produceret af Goddard Institute for Space Studies i New York, og distribueres frit fra NASA Langley Research Center, Distributed Active Archive Center, Hampton, Virginia, U.S.A.
REFERENCER
Bond, G., Kromer, B., Beer, J., Muscheler, R., Evans, M.N., Showers, W., Hoffmann, S., Lotti-Bond, R., Hajdas, I., Bonani, G., 2001. Persistent solar influence on North Atlantic climate during the Holocene. Science 294, 2130- 3136.
Borzenkova, I.I., Vinnikov, K.Ya., Spirina, L.P., Stekhnovskii, D.I., 1976. Variation of Northern Hemisphere Air Temperature from 1881 to 1975. Meteorologiya i Gidrologiya 7, 27-35.
Carslaw, K.S., Harrison, R.G., Kirkby, J., 2002. Cosmic Rays, Clouds, and Climate. Science 298, 1732-37.
DER SPIEGEL, 2. Juni 2001, pp. 196-201, viser Fig. 2 i Friis-Christensen og Lassen (1991), som i nærværende artikel er vist som Fig. 3.a.
Friis-Christensen, E., Lassen, K., 1991. Length of the solar cycle: An indicator of solar activity closely associated with climate. Science 254, 698-700.
Groveman, B.S., Landsberg, H.E., 1979a. Simulated northern hemisphere temperature departures 1579-1880. Geophysical Research Letters 6 (10), 767-769.
Groveman, B.S., Landsberg, H.E., 1979b. Reconstruction of northern hemisphere temperature: 1579-1880. Publication No. 79-181. University of Maryland.
Groveman, B.S., Landsberg, H.E. (1979c). Data Appendices to Publication No. 79-181. Publication No. 79-182. University of Maryland.
Haigh, J.D., 1996. The impact of Solar Variability on Climate. Science 272, 981-984.
Haigh, J.D., 2001. Climate variability and the influence of the Sun. Science 294, 2109-2111.
Jones, P.D., Raper, S.C.B., Bradley, R.S., Diaz, H.F., Kelly, P.M., Wigley, T.M.L., 1986. Northern hemisphere surface air temperature variations: 1851-1984. Journal of Climate and Applied Meteorology 25, 161-179.
Jones, P.D., 1988. Hemispheric surface air temperature variations: Recent trends and an update to 1987. Journal of Climate 1, 654-660.
Jones, P.D., Briffa, K.R., Tett, S.F.B., 1998. High-resolution palaeoclimatic records for the last millennium: interpretation, integration and comparison with General Circulation Model control-run temperatures. The Holocene 8 (4), 455-471.
Kernthaler, S., Toumi, R., Haigh, J., 1999. Some doubts concerning a link between cosmic ray fluxes and global cloudiness. Geophys. Res. Lett. 26, 863-865.
Kristjánsson, J.E., Kristiansen, J., 2000. Is there a cosmic ray signal in recent variations in global cloudiness and cloud radiative forcing? Journal of Geophysical Research 105 (D9) 11851-11863.
Kristjánsson, J.E., Staple, A., Kristiansen, J., 2002. A new look at possible connections between solar activity, clouds and climate. Geophysical Research Letters 29 (23) 2107-2110.
Lassen, K., Friis-Christensen, E., 1995. Variability of the solar cycle length during the past five centuries and the apparent association with terrestrial climate. Journal of Atmospheric and Solar-Terrestrial Physics 57 (8) 835-845.
Lassen, K., Friis-Christensen, E., 2000. Reply to the article “Solar cycle lengths and climate: A reference revisited” by P. Laut og J. Gundermann. J. Geophys. Res.-Space, 105 (A12) 27493-27495.
Laut, P., Gundermann, J., 1998. Solar cycle length hypothesis appears to support the IPCC on global warming. Journal of Atmospheric and Solar-Terrestrial Physics 60, 1719-1728
Laut, P., Gundermann, J., 2000a. Solar cycle lengths and climate: A reference revisited. Journal of Geophysical Research 105 (A12) 27489-92.
Laut, P., Gundermann, J., 2000b. Is there a correlation between solar cycle lengths and terrestrial temperatures? Old claims and new results. The First Solar and Space Weather Euroconference: The Solar Cycle and Terrestrial Climate. European Space Agency 189-191.
Mann, M.E., Bradley, R.S., Hughes, M.K., 1998. Globalscale temperature patterns and climate forcing over the past six centuries. Nature 392, 779-787.
Marsh, N.D., Svensmark, H., 2000. Low cloud properties influenced by cosmic rays. Physical Review Letters 85 (23) 5004-5007.
Marsh, N.D., Svensmark, H., 2002. GCR and ENSO trends in ISCCP-D2 low cloud properties. Journal of Geophysical Research. In press.
Shindell, D.T., Miller, R.L., Schmidt, G.A., Pandolfo, L., 1999. Simulation of recent northern winter climate trends by greenhouse-gas forcing. Nature 399, 452-455.
Shindell, D.T., Schmidt, G.A., Mann, M.E., Rind, D.,Waple, A., 2001. Solar Forcing of Regional Climate Change During the Maunder Minimum. Science 294, 2149-2152.
Svensmark, H., Friis-Christensen, E., 1997. Variation of cosmic ray flux and global cloud coverage - a missing link in solar-climate relationships. Journal of Atmospheric and Solar-Terrestrial Physics 59 (11), 1225-1232.
Svensmark, H., 1998. Influence of cosmic rays on Earth's climate. Physical Review Letters 22, 5027-5030.
Thejll, P., Lassen, K., 2000. Solar forcing of the Northern hemisphere land air temperature: New Data. Journal of Atmospheric and Solar-Terrestrial Physics 62, 1207-1213.
Udelhofen, P.M., Cess, R.D., 2001. Cloud cover variations over the United States: An influence of cosmic rays or solar variability? Geophys. Res. Lett. 28(13) 2617-2620.
Wagner, G., Livingstone, D.M., Masarik, J., Muschler, R., Beer, J., 2001. Some results relevant to the discussion of a possible link between cosmic rays and earth’s climate. J. Geophys. Res. 106, 3381-3387.
Yu, F., Turco, R.P., 2000. Ultrafine aerosol formation via ion-mediated nucleation. Geophysical Research Letters 27 (6), 883-886.
FIGURER
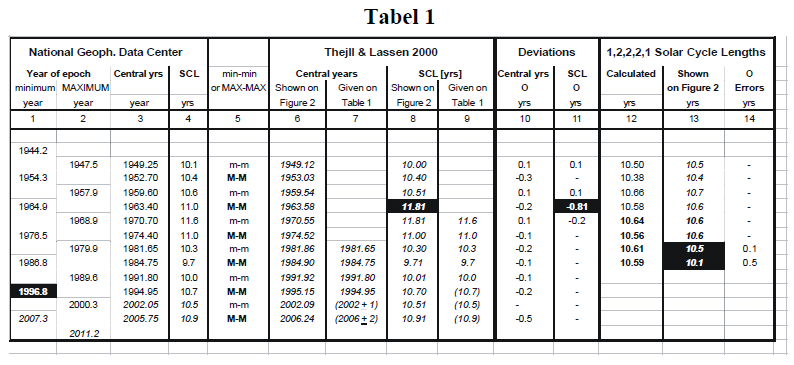
Tabel 1: En ajourført beregning af punkterne 1 - 4 på Fig. 3.a med påvisning af to væsentlige regnefejl i de numeriske beregninger i Lassen og Friis-Christensen (2000) og i Thejll og Lassen (2000).
I Friis-Christensen og Lassen (1991) var de sidste fire punkter på solcykluskurven (på Fig. 3.a markeret med numrene 1-4) afsat svarende til solcykluslængderne: 10.5, 10.3, 10.3 og 9.7 år. Da ordinataksen er valgt med orientering nedad afbildes denne række aftagende værdier som en stejl stigning på solcykluskurven. Denne stejle stigning giver en god overensstemmelse med temperaturkurven der afspejler de sidste årtiers kraftige globale opvarmning. Imidlertid hører punkterne 1-4 ikke hjemme på Fig. 3.a, idet de repræsenterer en anden type data end resten af kurven, dvs. de 20 forudgående punkter. Disse 20 punkter angiver 1,2,2,2,1-filtrerede data, dvs. kraftigt udglattede data, hvorimod punkterne 1 og 2 kun er delvist filtreret og punkterne 3 og 4 slet ikke er filtreret. Dette gør en forskel: Ikke-filtrerede solcyklusdata (dvs. de fysiske observationer uden udglatning) oscillerer voldsomt omkring den udglattede kurve. Som påvist af Laut og Gundermann (2000) skyldes den tilsyneladende fine overensstemmelse mellem solcykluskurven og de sidste årtiers globale opvarmning på Fig. 3.a ene og alene denne blanding af forskellige datatyper. Overensstemmelsen understøttes ikke af de fysiske observationer. Denne konklusion gælder såvel de data som er tilgængelige i dag som de data der var tilgængelige i 1991 da figuren først blev offentliggjort i en Science-artikel. I deres egen opdatering (Lassen og Friis-Christensen 2000) konstaterer forfatterne at “Med den information der er til rådighed i dag skulle de fire værdier have været 10.6, 10.6, 10.5 og 10.1" og “Substitution af de oprindelige data med de korrekte data ændrer imidlertid ikke indtrykket af en stejl stigning i solcykluskurven mellem 1970 og 1984". Disse konklusioner er imidlertid baseret på en regnefejl. Thejll og Lassen (2000) præsenterer de samme fire værdier (se søjle nr. 13 i ovenstående tabel) som resultatet af deres ajourføring der bygger på observerede (se søjle nr. 1 og 2) så vel som to forudsagte ekstremer for solpletantallet (se de sidste værdier i søjle nr. 1 og 2, trykt i kursiv). En korrekt beregning af de sidste to 1,2,2,2,1-vægtede gennemsnit giver de filtrerede værdier 10.61 og 10.59 (se søjle 12). Det kan man overbevise sig om ved simpelthen at regne efter, idet de af forfatterne anvendte SCL-værdier er opført i søjle 4: 1/8*10.6 +2/8*11.6 +2/8*10.3 +2/8*10.0 +1/8*10.5 = 10.61 og 1/8*11.0 +2/8*11.0 +2/8*9.7 +2/8*10.7 +1/8*10.9 = 10.59. Kontrolberegningen viser således at den ‘stejle stigning’ der præsenteres i begge artikler alene skyldes regnefejl i forfatternes numeriske beregninger. Fejlene berører udelukkende de to punkter nr. 3 og 4, som netop er dem der skaber den ‘stejle stigning’. Alle de øvrige numeriske resultater i deres ajourføring er korrekte. Den korrekte beregning med anvendelse af præcis de samme data (angivet i tabel 1 og på Fig. 2 hos Thejll og Lassen 2000) giver følgende resultater: 10.64, 10.56, 10.61 og 10.59 (se søjle nr. 12). Disse værdier udviser ikke noget spor af den postulerede ‘stejle stigning’.
I Tabel 1 er de vigtigste fejl fremhævet (se søjle nr. 13). For at gøre det lettere at sammenligne er tidspunktet, 1996.8, for solpletminimet som er anvendt af forfatterne bibeholdt selv om den observerede værdi er 1996.4 (se søjle 1).
Det skal bemærkes at værdierne fra den elektroniske digitalisering af figurerne (i søjlerne 6, 8 og 13) er angivet uden afrunding for ikke at indføre en ekstra kilde til usikkerhed.
Det skal også nævnes at grunden til at søjlerne 7 og 9 kun indeholder nyere værdier for hhv. de centrale år og SCL, er at det kun er disse der er medtaget i Table 1 i Thejll og Lassen (2000). Denne begrænsning betyder for øvrigt at tabellen ikke indeholder alle de SCL der er nødvendige for at kunne kontrollere punkterne på forfatternes Fig. 1 og Fig. 2 og fx påvise de to regnefejl. At der ikke er tale om at forfatterne har benyttet andre data end de NGDC-data der er angivet i søjlerne 1-4 i nærværende tabel fremgår af at alle de andre 1,2,1- og 1,2,2,2,1-gennemsnit på Fig. 1 og Fig. 2 er plottet med de værdier der opnås ved en korrekt beregning under benyttelse af disse NGDC-data.
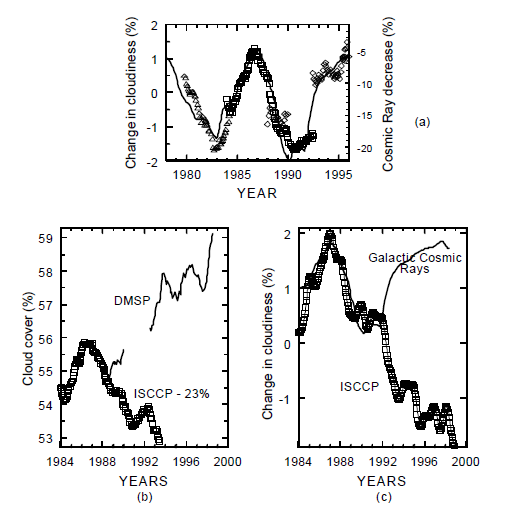
Figur 1: (a) Jordens ‘totale skydække’ og intensiteten af galaktisk kosmisk stråling som iagttaget ved Climax, Colorado (tynd optrukken linje, normeret til maj May 1965). Talværdierne er opnået ved scanning og digitalisering af Fig. 1 i Svensmark (1998). Trekanterne repræsenterer skydata fra NIMBUS-7 CMATRIX projektet for den Sydlige Halvkugle over havene ekskl. troperne. Kvadraterne viser ISCCP C2 og ISCCP D2 skydata målt fra geostationære satellitter over havene ekskl. troperne. Romberne er DMSP data som - iflg. Svensmark - repræsenterer “totalt skydække over havene på den Sydlige Halvkugle”. Såvel trekanterne, kvadraterne som romberne repræsenterer iflg. forfatteren “Jordens totale skydække”. (b) En sammenligning af to datasæt: DMSP-data og ISCCP-data for ‘totalt skydække’ som vist i Kristjánsson and Kristiansen (2000). Kvadraterne viser ISCCP-data, mens de to linjestykker der hhv. dækker perioderne 1988-1990 og 1992-1998 og løber op mod figurens højre hjørne viser DMSP-data. Den relative indbyrdes placering af disse to kurver kan vælges ret vilkårligt, dels fordi en indbyrdes kalibrering af måleserier fra forskellige satellitprogrammer næsten aldrig kan foretages særlig nøjagtigt, dels fordi disse to kurver repræsenterer helt forskellige fysiske størrelser. Sidstnævnte forhold fremgår bl.a. af at ISCCP- og DMSP-kurverne har helt forskellige forløb. I modsætning til de ISCCP- og DMSP-data der er vist på Fig. 1.a repræsenterer skydataene på Fig. 1.b det samme geografiske område. Herved opnås der en meningsfuld sammenligning. Det ses at i de tidsintervaller hvor kurverne overlapper falder det ‘totale skydække’ angivet ved ISCCP-serien, mens DMSP-seriens værdier samtidigt stiger. Den samme forskel udviser den samlede trend for hhv. ISCCP- og DMSP-serien. Derfor kan det konkluderes: at hvis det er korrekt at ISCCP-serien beskriver ‘totalt skydække’, så kan DMSP-serien umuligt også repræsentere ‘totalt skydække’. Teksten “ISCCP – 23 %” angiver at der er trukket 23 procentpoint fra ISCCP-dataene for at bringe dem nogenlunde på niveau med DSMP-værdierne. (c) Her ses en korrigeret og ajourført udgave af Fig. 1.a. Kvadraterne repræsenterer ISCCP-data og den optrukne kurve viser intensiteten af galaktisk kosmisk stråling som målt ved Climax, Colorado, udglattet som hos Kristjánsson and Kristiansen (2000). Korrektionen består i at samtlige DMSP-data er fjernet idet de slet ikke repræsenterer ‘totalt skydække’ og derfor ikke hører hjemme i nærværende sammenhæng. Ajourføringen består i at nye data for ‘totalt skydække’ er tilføjet fra http://isccp.giss.nasa.gov/ climanal1.html (2001).
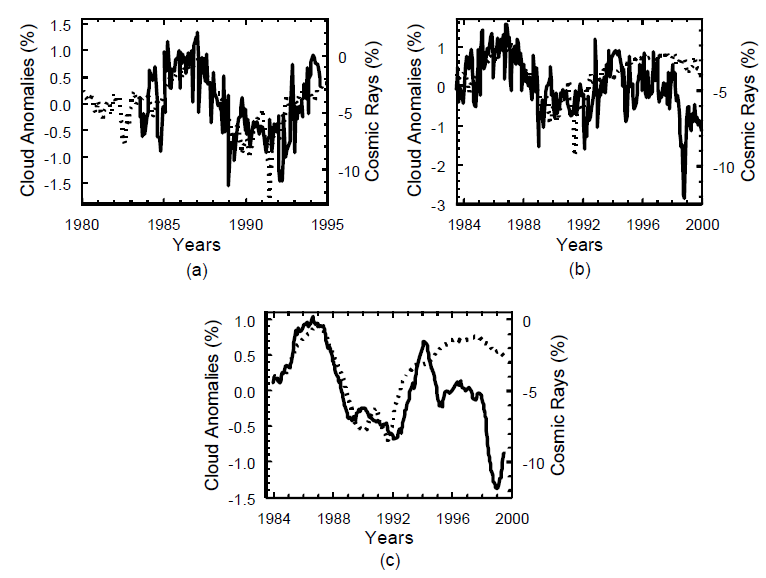
Figur 2: (a) Lavt skydække (tyk linje) og intensiteten af galaktisk kosmisk stråling som målt ved Huancayo (tynd linje) iflg. Marsh og Svensmark (2000). (b) Lavt skydække (tyk linje) og intensiteten af galaktisk kosmisk stråling som målt ved Huancayo (tynd linje) iflg. Kristjánsson et al. (2002). (c) Som på Fig. 2.b men udglattet for at trenden træder tydeligere frem.
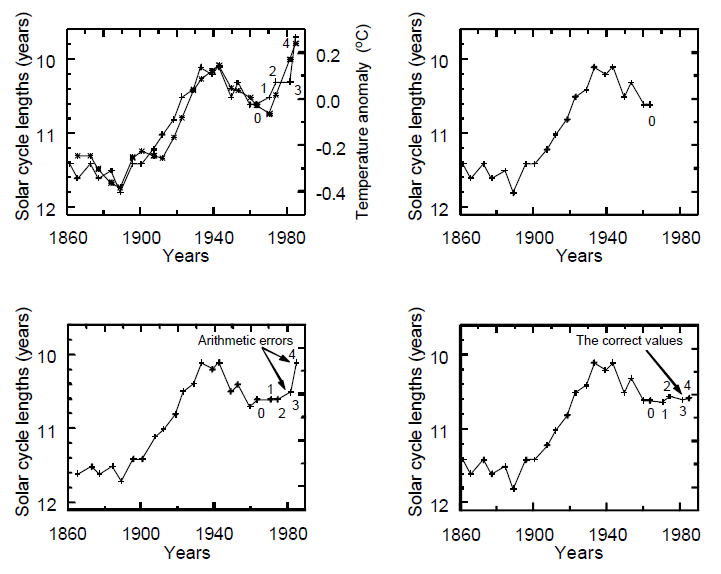
Figur 3: (a) Solcykluslængder, SCL, (kurve med + tegn) og overfladetemperaturer over land på den Nordlige Halvkugle (kurve med * tegn). Her vises de værdier Friis-Christensen og Lassen præsenterede som Fig. 2 i deres oprindelige Science-artikel fra 1991 (i rekonstruktion). For en ordens skyld skal det lige bemærkes at SCL ikke er afsat ækvidistante. Det skyldes at de enten er afsat midt imellem to solpletminima eller to maksima, og da afstanden mellem disse varierer noget kommer ‘centerårene’ til at ligge noget uregelmæssigt. ‘Solkurvens’ første 20 punkter er 1,2,2,2,1-filtrede solcykluslængder, og dens sidste fire punkter (markeret 1-4) markerer solcykluslængder der kun er filtreret delvist (punkterne 1-2) eller slet ikke (punkterne 3-4). Den stejle stigning som de to sidste punkter udviser skyldes simpelthen at de er plottet direkte som observerede solcykluslængder, altså uden filtrering (eller udglatning), og at sådanne ikke-filtrerede solcykluslængder danner en kurve med voldsomme udsving op over og ned under den kraftigt udglattede kurve der dannes af de 1,2,2,2,1-filtrerede solcykluslængder. Punkterne 3 og 4 er simpelthen en del af et sådant udsving op over den udglattede kurve. Det er alene denne blanding af forskellige datatyper der skaber det fejlagtige indtryk at solcykluslængdernes udvikling i de senere årtier meget fint svarer til den observerede globale opvarmning. (b) Her ses hvordan kurven burde have været offentliggjort i 1991, uden sammenblanding af forskellige datatyper. Her er solcykluskurven udelukkende bestemt ved data som rent faktisk var observeret på dette tidspunkt. Det punkt der er markeret med ‘0' angiver den sidste korrekt 1,2,2,2,1-filtrerede værdi. (c) Dette er en ajourført udgave af solcykluskurven med de værdier der præsenteres i Lassen og Friis-Christensen (2000) samt Thejll og Lassen (2000). Lassen og Friis-Christensen gør især opmærksom på den ‘stejle stigning’ som kurvens to sidste punkter, 3 og 4, udviser og ser den som udtryk for at også den ajourførte solcykluskurve viser en fin overensstemmelse med den globale opvarmning. En kontrolberegning viser imidlertid at den stigning som punkterne 3 og 4 udviser, alene skyldes fejl i de numeriske beregninger. En korrekt gennemført beregning på grundlag af de data som specificeres i Thejll og Lassen fører til det flade kurveforløb der er vist på Fig. 3.d. Bortset fra punkterne 3 og 4 er alle andre talværdier (inkl. punkterne 1-2) hos Thejll og Lassen beregnet korrekt. Forfatterne har dog foretaget visse afrundinger, mens Fig. 3.d. er mere præcis. Dette forklarer de små afvigelser mellem kurverne som ses ved en sammenligning af Fig. 3.c og Fig. 3.d. (d) Her ses en (korrekt beregnet) opdatering af den oprindelige solcykluskurve (Fig. 3.a), nu med punkterne 1-4 beregnet under benyttelse af de samme observerede og forudsagte data som også anvendes af Thejll og Lassen (2000). Bemærk, at de nye solcyklusdata danner en flad kurve der ikke på nogen måde afspejler de seneste årtiers globale opvarmning.
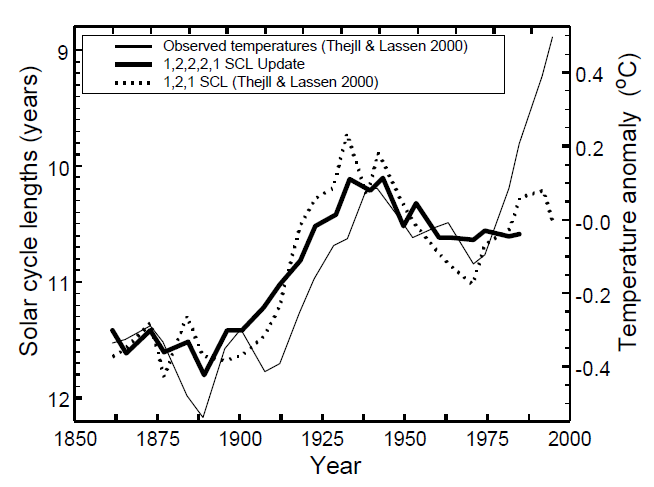
Figur 4: Observerede temperaturer (tynd linje) og 1,2,1-filtrerede solcykluslængder (punkteret linje) som vist på Fig. 3 i Thejll og Lassen (2000). 1,2,2,2,1-filtrerede solcykluslængder som vist på Fig. 2 i Friis-Christensen og Lassen (1991) med de sidste fire punkter opdateret (tyk linje).
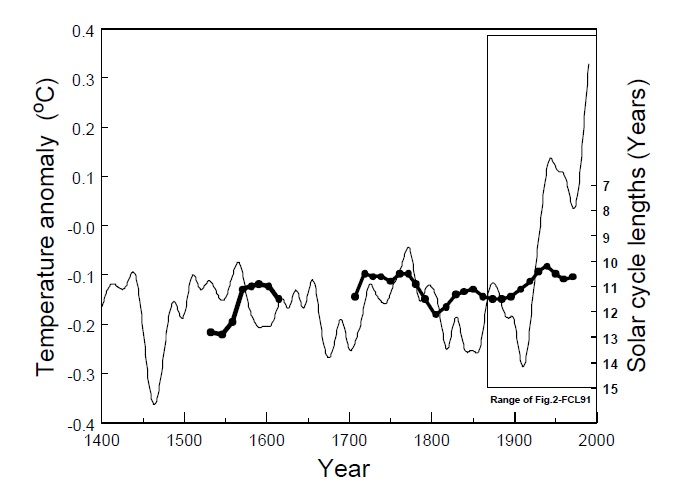
Figur 5: 1,2,2,2,1-filtrerede minimum-minimum solcykluslængder (kurven med de udfyldte cirkler) og temperaturerne på den Nordlige Halvkugle (kurven uden symboler). Fig. 5 viser i det væsentlige de samme fysiske størrelser som Fig. 3.a, men her er de sammenlignet over en længere tidsperiode. Bemærk at en lineær regression som regel giver en langt dårligere overensstemmelse mellem solcykluslængder og terrestriske data når sammenligningen udstrækkes over et længere tidsinterval hvor hver af kurverne indeholder et større antal specifikke detaljer. Den indsatte ramme markerer det interval som Fig. 3.a spænder over. Det er værd at bemærke at mens en indbyrdes skalering som den i Fig. 3.a benyttede, anvendt på Fig. 4, ville forbedre overensstemmelsen mellem de to kurvers ’S-faconer’ inden for rammen, ville den samtidig give en meget dårligere kurvetilpasning uden for rammen. Fx ville afvigelsen mellem solcykluskurvens ‘top’ og temperaturkurvens samtidige ‘dal’ omkring år 1600 forøges.
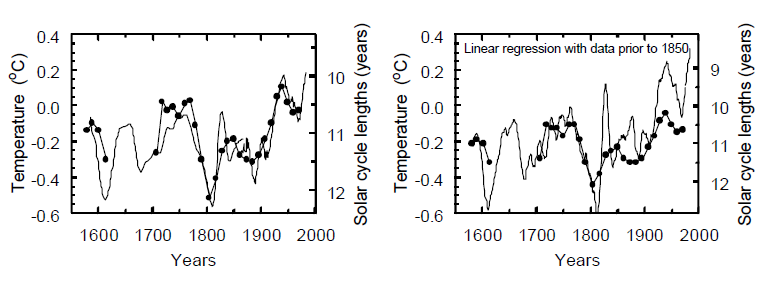
Figur 6: (a) 1,2,2,2,1-filtrerede minimum-minimum solcykluslængder (linje med udfyldte cirkler) og to forskellige serier for overfladetemperaturen over land på den Nordlige Halvkugle: Grovemann / Landsberg der løber fra 1585 til 1866 (punkteret linje) og Jones der løber fra 1862 til 1982 (optrukken linje). Kurverne overlapper i perioden fra 1862 til 1866, hvor de forløber stort set parallelt i en afstand på omkring 0.1 ºC. Den tilsyneladende gode overensstemmelse mellem de to temperaturkurver og solcykluskurven er opnået på følgende vis: (1) De to serier er afbildet i to forskellige temperaturskalaer. Herved sænkes den højre kurve ca. 0.1 ºC i forhold til den venstre kurve, og den globale opvarmning, over det tidsrum kurven spænder over, mindskes tilsyneladende med en tredjedel. (2) Forfatterne har løftet hele solcykluskurven så meget at den stemmer godt overens med den højre del af temperaturkurven. Denne tilpasning er sket på bekostning af de ældre data. Virkningen kan umiddelbart aflæses af figuren: Solcykluskurvens punkter ligger på venstre side af figuren gennemgående højt over temperaturkurven. Hvis tilpasningen var sket ved lineær regression ville nogle af dens punkter ligge over, nogle under temperaturkurven. (b) Her er solcykluskurven (linje med udfyldte cirkler) den samme som på Fig. 6.a, men de to forskellige temperaturserier med værdier angivet i hver sin temperaturskala er her erstattet af Groveman / Landsberg / Borzenkova-serien for 1579-1975 (optrukken linje), hvis værdier alle er angivet i samme temperaturskala. For at lette sammenligningen er Groveman / Landsberg / Borzenkova - kurven ajourført med nulpunktskorrigerede Jones-data for årene 1975-82 således at kurverne slutter i samme år. Kurvetilpasningen er her opnået ved simpel lineær regression, idet der dog kun er benyttet data fra før 1850. Dette er sket for at undgå at en eventuel Sol/Jord-korrelation ‘sløres’ af en temperaturpåvirkning fra de menneskeskabte drivhusgasser.
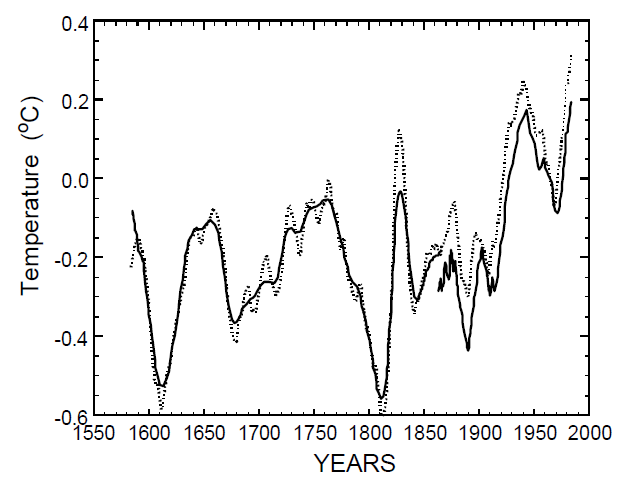
Figur 7: Den punkterede linje viser et 11-års løbende gennemsnit af Groveman / Landsberg / Borzenkovatemperaturserien 1579-1975 som præsenteret i Groveman og Landsberg (1979). Den tykke kurve til venstre viser en forenklet udgave af et 11-års løbende gennemsnit af Groveman / Landsberg / Borzenkovatemperaturserien fra 1585 til 1866 som er anvendt i Lassen og Friis-Christensen (1995). Kurvens nøjagtige definition er uklar da den ikke stemmer overens med forfatternes egen beskrivelse. Den tykke kurve til højre viser et 11-års løbende gennemsnit af en temperaturserie fra 1862 til 1982 publiceret af Jones et al. (1986), Jones (1988) og Jones et al. (1998). Jones’ temperaturkurve beskriver en temperaturudvikling som er meget lig den tilsvarende del af Groveman / Landsberg / Borzenkova-kurven, lige bortset fra at den er forskudt 0.1 ºC nedad fordi Jones’ serie anvender en anden temperaturskala med et højere nulpunkt. For at lette sammenligningen er Groveman / Landsberg / Borzenkova - kurven ajourført med nulpunktskorrigerede Jonesdata for årene 1975-82 således at kurverne slutter i samme år.
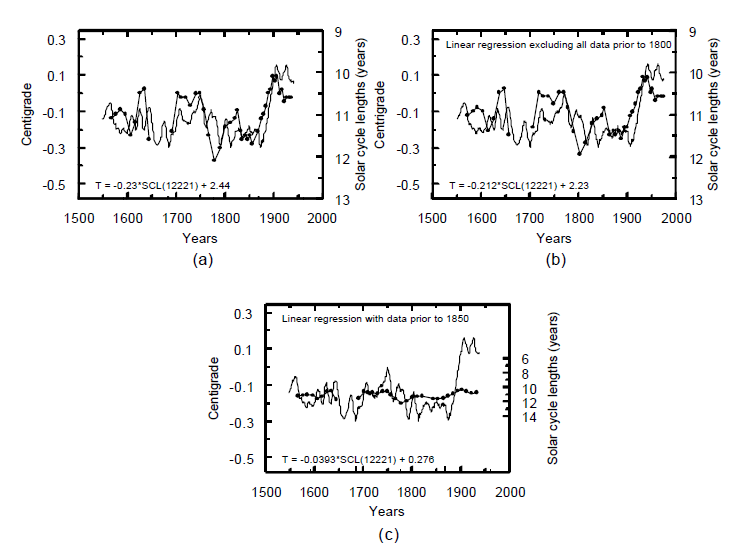
Figur 8: (a) Solcykluslængder (linje med cirkler) sammenlignet med overfladetemperaturer over land på den Nordlige Halvkugle som præsenteret i Lassen og Friis-Christensen (2000). Tætheden af soldata efter år 1850 er blevet fordoblet idet der her (foruden minimum-minimum solcykluslængderne) også er medtaget maksimum-maksimum solcykluslængder. Herved opnås der en god tilpasning med solcykluskurven over netop den tidsperiode hvor der er mistanke om at en menneskeskabt opvarmningstrend ligger overlejret over Jordens naturlige temperaturfluktuationer. De dele af temperaturkurven der ikke er påvirket af menneskeskabte drivhusgasser, opviser kun en dårlig overensstemmelse med solcykluskurven. Det betyder at den delvise overensstemmelse mellem kurverne, som figuren viser, måske er en følge af følgende to faktorer: (1) en vis, tilfældig overensstemmelse mellem solcykluskurvens form og den måde hvorpå menneskelig aktivitet har udviklet sig og (2) den omstændighed at der ved kurvetilpasningen stort set ikke tages hensyn til observationer der ligger før den industrielle revolution. Denne problematiske udnyttelse af de to kurvers ‘S-faconer’ illustreres også af Fig. 5 ovenfor, hvor solkurvens flade ‘S-facon’ kan skaleres op således at den stemmer fint overens med temperaturkurvens stejle ‘S-facon’ inden for den indsatte ramme. (b) Her ses resultatet af en kontrolberegning der blev gennemført for at finde ud af hvilke numeriske vægte Lassen og Friis-Christensen (2000) har tildelt de ældre solcyklusdata. Forfatterne oplyser nemlig ikke de af dem indførte talværdier, og det er derfor ikke umiddelbart muligt at reproducere deres resultater. Fig. 8.b er opnået (efter en række forgæves forsøg) ved at sætte vægtfaktoren for samtlige solcykluslængder fra før år 1800 til nul. Den herved opnåede figur er praktisk taget identisk med forfatternes egen Fig. 8.a. Deres valg af vægtfaktorer er derfor ækvivalent med at der er set bort fra samtlige soldata før år 1800. Hvis disse vægtfaktorer virkelig er sat til nul skal der mindes om at man i videnskabelig sammenhæng normalt vil udelade data der fortjener en vægtfaktor på nul. Når data er så upålidelige at der overhovedet ikke kan tages hensyn til dem i en lineær regression bør de nok slet ikke præsenteres på en graf sammen med gyldige fysiske data, eller i hvert fald ikke uden at læseren informeres herom og advares mod at tillægge dem nogen betydning. Den fremgangsmåde der anvendes i forbindelse med Fig. 8.a kan beskrives således: Først tvinges solcykluskurven og temperaturkurven til at stemme overens netop i perioden 1870-1960, hvor temperaturkurven kan være præget af en menneskeskabt global opvarmning. Og så præsenteres den fine overensstemmelse over denne periode (over kurvernes to ‘S-faconer’) som indikation på at den globale opvarmning skyldes Solen og ikke menneskelige aktiviteter. (c) Her er kurvetilpasningen af de samme data som på Fig. 8.a og Fig. 8.b foretaget ved lineær regression, idet dog den kunstige fordobling af data over ‘S-faconen’, ved tilføjelse af maksimum-maksimum solcykluslængder, er udeladt. De første 230 år af solcyklusserien er her medtaget og med samme vægt som de øvrige soldata. Her har de altså ikke fået tildelt vægtfaktoren nul. For at mindske faren for at en evt. korrelation mellem de solare og terrestriske data kan blive sløret af en mulig menneskeskabt opvarmning er kun data før 1850 anvendt i den lineære regression.
Af Peter Laut, Institut for Fysik, Danmarks Tekniske Universitet
1. BAGGRUND
Inden for det sidste årti er der offentliggjort en række videnskabelige artikler der hævder at have påvist stærke korrelationer mellem forskellige indikatorer for solaktiviteten og nogle parametre for Jordens klima: Det er således blevet hævdet at der skulle eksistere en fin overensstemmelse mellem galaktiske kosmiske strålers intensitet og jordens skydække, først gældende for det totale skydække og derefter ændret til alene at gælde lave skyer, og en fin overensstemmelse mellem solcykluslængder og overfladetemperaturen over land på den Nordlige Halvkugle. Disse korrelationer spiller en betydelig rolle i såvel den videnskabelige litteratur som i den offentlige debat vedrørende risikoen for en menneskeskabt klimaændring. Jeg har analyseret en række af artiklernes centrale grafer. Disse skulle dokumentere de stærke korrelationer, og flere af dem har spillet en væsentlig rolle i klimadebatten og er blevet taget til indtægt for den opfattelse at den observerede globale opvarmning i overvejende grad skyldes Solen. Mine analyser viser imidlertid at de tilsyneladende stærke korrelationer som graferne viser er opnået ved en ukorrekt håndtering af de fysiske data. Jeg mener derfor at graferne ikke kan anvendes som grundlag for konklusioner mht. spørgsmålet om hvorvidt menneskeheden bør eller ikke bør mindske udslippene af drivhusgasser.
Jeg vil gerne understrege at mine analyser ikke på nogen måde udelukker at der eksisterer sammenhænge mellem Solens aktivitet og klimaet på Jorden. Sådanne forbindelser er i årenes løb blevet påvist af mange forskere. Men en signifikant sammenhæng mellem Solens aktivitet og de sidste 140 års globale opvarmning er endnu hverken blevet påvist eller sandsynliggjort. Mit formål med nærværende analyse er således ikke at bevise at Solens aktivitet ikke påvirker eller har påvirket Jordens klima, men blot at gøre opmærksom på at nogle af de figurer der vises igen og igen i videnskabelige artikler, avisindlæg, skolebøger og tv-udsendelser, slet ikke stemmer overens med de fysiske observationer.
Det er følgende artikler jeg har koncentreret mig om:
- En artikel som de to danske forskere Eigil Friis-Christensen og Knud Lassen offentliggjorde i året 1991 og som syntes at påvise en stærk korrelation mellem solcykluslængder og overfladetemperaturen over land på den Nordlige Halvkugle i perioden 1860-1990.
- En tilsvarende analyse for en udvidet periode 1579- 1987 som Lassen og Friis-Christensen præsenterede i året 1995, og
- en opdatering af de samme korrelationer fra året 2000 af de samme forfattere, som svar på en kritisk artikel ved Laut og Gundermann (2000). Jeg refererer også kort til en artikel som de to danske forskere Peter Thejll og Knud Lassen offentliggjorde på stort set samme tid. Den indeholdt nogle af de samme opdateringer som Lassen og Friis-Christensen (2000).
- En artikel som den danske forsker Henrik Svensmark offentliggjorde i 1998. Den præsenterer satellitobservationer af skydata som synes at vise at ‘det totale skydække’ er stærkt korreleret med intensiteten af galaktisk kosmisk stråling (GCRI). Resultaterne var oprindeligt offentliggjort af Svensmark og Friis-Christensen i 1997, men da det hovedsageligt er en figur fra 1998-artiklen der refereres til, er det den jeg har analyseret.
- I året 2000 præsenterede Marsh og Svensmark (2000) en ny hypotese der gik ud på at det var ‘dækket af lave skyer’ (og altså ikke ‘det totale skydække’ som hævdet i Svensmark 1998), der korrelerede stærkt med den kosmiske stråling. Alle disse artikler indeholdt grafer der viste stærke korrelationer mellem fysiske størrelser der beskrev forhold på hhv. Solen og Jorden.
I det følgende vil jeg diskutere artiklerne i en rækkefølge der afspejler deres grad af aktuel almen interesse.
Ved diskussionen af de publicerede grafer har jeg her valgt at anvende “rekonstruktioner” af de originale figurer, dvs. at jeg har scannet og digitaliseret figurerne elektronisk og derefter plottet de aflæste værdier. Denne fremgangsmåde muliggør en enkel og nøjagtig sammenligning af talværdierne samt giver mulighed for at plotte dem i forskellige formater og farver med henblik på at lette struktureringen og diskussionen af graferne. I visse tilfælde er layoutet imidlertid valgt på en sådan måde at graferne, for alle praktiske formål, er identiske med originalerne.
2. NOGLE SOLHYPOTESER
2.1 “Det totale skydække korrelerer stærkt med intensiteten af galaktisk kosmisk stråling
I året 1997 offentliggjorde Svensmark og Friis-Christensen en artikel hvori de mente at have påvist en stærk korrelation mellem det totale skydække og intensiteten af galaktisk kosmisk stråling som målt ved Climax, Colorado. Denne artikel blev opdateret af Svensmark i 1998. Artiklernes hovedresultat er illustreret ved sidstnævnte artikels Fig. 1. Nedenstående Fig. 1.a er en rekonstruktion af den oprindelige graf opnået som beskrevet ovenfor. Hvis der skulle være opstået mindre afvigelser fra originalen skyldes det at denne er noget utydelig: Nogle områder på originalen er dækket af så megen tryksværte at det er umuligt at aflæse hvilke datasymboler der er afsat. Denne usikkerhed skyldes det store format der er valgt til symbolerne. Eksempelvis er det ikke muligt at afgøre om dataene fra Defense Meteorological Satellite Program (DMSP)1 - som repræsenteres ved romber - i årene 1990-92 følger den ‘hængekøjefacon’ som den kosmiske stråling angiver, eller om de i det mindste følger den nedadgående tendens som både den kosmiske stråling og ISCCP-dataene2 følger. Disse spørgsmål er naturligvis vigtige hvis man vil finde ud af om DMSP-dataene overhovedet hører hjemme på denne graf, om de overhovedet repræsenterer totalt skydække, dvs. den samme fysiske størrelse som ISCCP-dataene. På figuren kan der tydeligt skelnes romber fra 1988-90 og fra 1992- 1995, men den originale figur fra Svensmark (1998) tillader ikke at afgøre om de også bidrager til det stærkt sværtede område i perioden 1990-92. Her kommer heldigvis nogle analyser til hjælp der er foretaget af de to norske forskere Kristjánsson og Kristiansen (2000). De gør det muligt at fastslå at DMSP-dataene i virkeligheden har et forløb der hverken stemmer overens med ‘det totale skydække’ eller med kosmisk stråling.
Bemærk i øvrigt at Svensmarks figur for det meste af år 1992 synes at indikere at det totale skydække på en og samme tid skulle have været usædvanligt beskedent (iflg. den lave kurve) og usædvanligt kraftigt (iflg. den høje kurve).
Fig. 1.b viser en sammenligning af DMSP-dataene med ISCCP’s data for totalt skydække som præsenteret i Kristjánsson og Kristiansen (2000). Fig. 1.b er en rekonstruktion af deres originale figur, idet deres data her er vist i samme layout som Svensmarks figur for at muliggøre en direkte sammenligning. Figuren viser at de to dataserier, DMSP og ISCCP, forløber helt forskelligt. I de tidsintervaller hvor de overlapper aftager det totale skydække iflg. ISCCP samtidigt med at DMSP-værdierne vokser. Det samme gælder de to seriers samlede trend. Hvis man derfor antager at ISCCP-serien giver et korrekt billede af det totale skydækkes udvikling i tiden, kan DMSP-dataene umuligt også repræsentere totalt skydække.
Fig. 1.c er en korrigeret og ajourført version af Svensmarks originale figur (her reproduceret som Fig. 1.a). Korrektionen består i fjernelsen af DMSP-dataene, der jo er irrelevante her da de ikke repræsenterer totalt skydække. Ajourføringen består i en tilføjelse af nyere data for totalt skydække fra http://isccp.giss.nasa.gov/climanal1.html (ISCCP D2 data for perioden 1983-99, udglattet med en båndbredde svarende til Fig. 1.a). Derudover viser figuren også den kosmiske stråling (GCRI) som målt ved Climax i Colorado. Figuren viser at det totale skydække stemmer ganske fint overens med den kosmiske stråling i perioden 1985-89 hvorefter kurverne går hver sin vej: det totale skydække falder kraftigt i de efterfølgende år mens intensiteten af den kosmiske stråling stiger kraftigt.
Analyserne i Kristjánsson og Kristiansen (2000) viser at perioden med overensstemmelse (1985-89) blev udvidet kunstigt på Fig. 1.a ved at kombinere to dataserier der repræsenterer to forskellige fysiske størrelser (ISCCP og DMSP) på en sådan måde at de giver indtryk af at danne en enkelt sammenhængende kurve. Der er altså tale om det der på jævnt dansk kaldes “at blande æbler og pærer”. Fig. 1.a har spillet en vigtig rolle både i den videnskabelige litteratur og i den offentlige debat om de mulige årsager til den globale opvarmning.
2.2 “Lavt skydække korrelerer stærkt med intensiteten af galaktisk kosmisk stråling
” I året 2000 præsenterede Marsh og Svensmark (2000) en ny hypotese der gik ud på at det var ‘dækket af lave skyer’ (og altså ikke det ‘totale skydække’ som hævdet i Svensmark 1998), der korrelerede stærkt med den kosmiske stråling, som i deres artikel var repræsenteret ved data fra den peruvianske observations-station Huancayo. Den centrale graf (Fig. 1.c) i deres artikel er i nærværende artikel gengivet som Fig. 2.a (igen en rekonstruktion). Fig. 2.b viser en opdatering ved Kristjánsson et al. (2002) og Fig. 2.c en udglattet version af sidstnævnte kurve. En sammenligning med Fig. 2.a giver anledning til en række kommentarer:
(1) Overensstemmelsen mellem det lave skydække og kosmisk stråling er ikke god efter år 1989, og efter år 1994 er der absolut ingen overensstemmelse.
(2) Ved første øjekast synes den stejle stigning af det lave skydække efterår 1992 (se fx Fig. 2.c) at svare ganske godt til en tilsvarende stigning i den kosmiske stråling. Imidlertid er stigningen i det lave skydække mere end et halvt år forsinket i forhold til den kosmiske stråling. Ifølge gældende teori (fx Yu og Turco 2000) skulle den udvikling af kondensationskerner for skydannelsen, der har ionerne fra den kosmiske stråling som kim, være tilendebragt mindre end et døgn efter at en stigning i den kosmiske stråling har fundet sted. Og da levetiden af sådanne aerosoler (kondensationskerner) kun beløber sig til nogle få dage må en evt. skydannelse finde sted inden for denne tidshorisont og ikke flere måneder senere. En skydannelse der sker som respons på ændringer i kosmisk stråling, må derfor fremtræde som praktisk taget samtidigt med ændringerne i den kosmiske stråling når den afbildes i den tidsskala der anvendes på Fig. 2.
(3) En anden vanskelighed er den fysiske tolkning af infrarød data fra satellitobservationer til bestemmelse af det lave skydække: Lave skyer der befinder sig neden under højere skyer kan ofte slet ikke observeres fra satellitter, og da den relative variation af de forskellige skytyper kun andrager nogle få procent kan selv en beskeden fejl ved bestemmelsen af det lave skydække påvirke kurveforløbet på en væsentlig og samtidig tilfældig måde, således at sammenligninger med andre kurver bliver meningsløse.
Kernthaler et al. (1999) har studeret forskellige typer skyer og har ikke fundet nogen overensstemmelse mellem de enkelte skytyper og kosmisk stråling. Wagner et al. (2001) har sammenlignet en ‘proxy’ for kosmisk stråling, nemlig koncentrationer af isotoperne 10Be og 36Cl, med ‘proxy’er’ for Jordens klima, 018O- og CH4-koncentrationen, over tidsperioden fra 20.000 til 60.000 år før nu og ikke fundet nogen korrelation. Kristjánsson et al. (2002) har sammenlignet korrelationen af det lave skydække med hhv. solarkonstanten (= total solar irradiance) og GCRI og fundet at korrelationskoefficienten med total solar irradiance er langt den største (r = 0.80 mod r = 0.47). Dette resultat kunne pege i retning af at solaktiviteten måske virkeligt påvirker udstrækningen af det lave skydække, men at den fysiske mekanisme i virkeligheden er knyttet til ændringer i Solens elektromagnetiske udstråling, og ikke til kosmisk stråling. Det ville stemme godt overens med en mekanisme der har været diskuteret i de senere år (Bond et al. 2001, Haigh 2001, Shindell et 1999, 2001) hvor det antages at temperaturændringer i stratosfæren, forårsaget af ændringer i Solens ultraviolette bølgelængder (ændringer som relativt er betydeligt større end ændringerne i det synlige område), giver anledning til en dynamisk respons i troposfæren som måske kan påvirke Jordens klima. Muligvis spiller planetariske bølger en vigtig rolle ved disse processer. Derfor kan den delvise overensstemmelse mellem det lave skydække og GCRI som vises i Marsh og Svensmark (2000) skyldes den omstændighed at GCRI og solarkonstanten begge er fysiske størrelser der er knyttet til solaktivitet, og at en årsagssammenhæng mellem det lave skydække og solarkonstanten automatisk vil medføre en vis, men mindre grad af overensstemmelse med GCRI, selv i det tilfælde hvor kosmisk stråling ikke spiller nogen rolle ved de fysiske processer der fører til dannelsen af lave skyer.
En alternativ forklaring af den dårlige overensstemmelse mellem GCR og det lave skydække efter 1994 (som vist på Fig. 2.b and Fig. 2.c) er fremsat af Marsh og Svensmark (2002), der hævder at den manglende overensstemmelse er et artefakt der skyldes problemer med instrumentkalibreringen mellem september 1994 og januar 1995. En diskussion af mulige forklaringer og mulige fysiske processer er givet af Carslaw et al. (2002).
Da variationen af den ultraviolette udstråling fra solen over de sidste 100 år ikke er kendt, og da mekanismerne for dens mulige klimapåvirkning ikke er afklaret, ikke mindst graden af nonlinearitet, er det endnu ikke muligt at afgøre hvorvidt disse processer har bidraget til den globale opvarmning som Jorden har oplevet over denne periode.
2.3 “Solcykluslængder korrelerer kraftigt med overfladetemperaturen over land på den Nordlige Halvkugle (1991)”
I 1991 offentliggjorde Friis-Christensen og Lassen i det ansete videnskabelige tidsskrift Science en artikel hvori de mente at have påvist en “slående god overensstemmelse” mellem solcykluslængder (SCL) og lufttemperaturen ved overfladen over den Nordlige Halvkugles landområder. Artiklen vakte stor opmærksomhed over hele verden og bliver stadigvæk ofte citeret i den videnskabelige litteratur. En søgning i Science Citation Index Expanded fra Institute for Scientific Information viser at artiklen er blevet citeret 213 gange fra 1991 til september 2002. I den senere tid er den blevet citeret en eller to gange om måneden. Også i den offentlige debat om de mulige årsager til den globale opvarmning spiller den stadigvæk en stor rolle (se fx DER SPIEGEL 2001). Artiklens centrale figur (Fig. 2 i Science-artiklen; fx gengivet i Vejret nr. 1, 1992) er i nærværende artikel vist som Fig. 3.a der igen er en rekonstruktion - her med tilføjelse af en nummerering (fra 0 - 4) af nogle kurvepunkter for at lette struktureringen og diskussionen. Af særlig interesse er den meget fine overensstemmelse mellem de seneste årtiers kraftige globale opvarmning og den tilsvarende stejle stigning i solcykluskurven. Den offentlige debat har netop fokuseret på de seneste årtiers markante globale opvarmning, og den tilsyneladende overensstemmelse mellem temperaturkurven og solkurven har overbevist mange mennesker om at det er solen, og ikke menneskeskabte drivhusgasser, der har været årsagen til denne opvarmning.
En omhyggelig analyse afslører imidlertid nogle problematiske detaljer: Figurens solcykluskurve består af i alt 24 punkter. Heraf er de første 20 punkter “1,2,2,2,1- filtrerede” værdier, dvs. at de er beregnet som løbende gennemsnit over fem på hinanden følgende observerede maksimum-maksimum eller minimum-minimum solcykluslængder med vægtfaktorerne: 1/8, 2/8, 2/8, 2/8, 1/8. Hvert af disse 20 punkter repræsenterer altså observationer over et tidsinterval på omkring 55 år (5 gange den gennemsnitlige solcykluslængde på 11 år). Det betyder at for hvert punkt der afsættes kræves der et kendskab til udviklingen af solpletantallet ca. 28 år ud i fremtiden og 28 år bagud i tiden. Kurvens første 20 punkter er altså fremkommet som resultat af en meget kraftig udglatning (eller ‘filtrering’) af de observerede data. Sammenligner man denne udglattede kurve med de ikke-filtrerede solcykluslængder, dvs. med de observerede data, finder man at de ikke-filtrerede værdier udfører voldsomme svingninger op over og ned under den udglattede kurve. Punkterne nr. 3 og 4 på Fig. 3.a repræsenterer sådanne ikke-filtrerede solcykluslængder, medens punkterne nr. 1 og 2 repræsenterer data som kun er delvist filtreret. Den tilsyneladende overensstemmelse mellem solkurven og temperaturkurven er opnået kunstigt ved at kombinere den udglattede kurves 20 punkter med det seneste opsving i den række af kraftige udsving op og ned som de observerede solcykluslængder udviser, dvs. ved at kombinere forskelligartede fysiske datasæt, eller sagt på jævnt dansk: ved at ‘blande æbler og pærer’. Hvis man i stedet for havde kombineret den udglattede kurve med et udsving nedad ville solcykluskurven i stedet have stemt fint overens med en dramatisk global afkøling. Denne kombination kunne man så have valgt hvis en sådan global afkøling havde fundet sted (Problemet diskuteres detaljeret i Laut og Gundermann 2000). Dette demonstrerer at det kan give misvisende resultater at blande forskellige typer data på denne måde. For at undgå en sådan sammenblanding burde de sidste fire punkter have været udeladt i den oprindelige publikation. Herved var solcykluskurven kommet til at se ud som vist på Fig. 3.b, hvor den ender i punkt nr. ‘0': Dette punkt markerer den sidste solcyklusværdi der på tidspunktet for artiklens offentliggørelse i 1991 kunne beregnes korrekt, dvs. ved en 1,2,2,2,1-filtrering.
I dag, hvor der i mellemtiden er kommet flere observationer, kan kurven forlænges ud over punkt ‘0'. Fig. 3.c viser den opdaterede solcykluskurve med de nye (1,2,2,2,1-filtrerede) punkter nr. 1 - 4 tilføjet. Lassen og Friis-Christensen (2000) og Thejll og Lassen (2000) præsenterer også opdaterede værdier for disse fire punkter, men ved nærmere eftersyn viser det sig at opdateringerne til dels er præget af regnefejl. Begge artikler anvender dels de to solcykluslængder der i mellemtiden har kunnet måles og dels forudberegnede værdier for tidspunkterne for det næste solpletminimum og det næste solpletmaksimum. Begge artikler benytter nøjagtigt de samme data, og disse er også anvendt til beregning af Fig. 3.d (se Tabel 1 nedenfor). Thejll og Lassen (2000) præsenterer deres opdaterede værdier såvel i deres Fig. 1 og i Fig. 2. Fig. 3.c viser hvordan solcykluskurven med deres fejlbehæftede opdatering kommer til at se ud. Det er punkterne 3 og 4 der er behæftede med simple numeriske regnefejl, og det er alene takket være disse regnefejl at kurven opnår den stejle stigning som passer så fint med de sidste årtiers globale opvarmning. Man kan overbevise sig selv om regnefejlen ved simpelthen at regne efter. De 1,2,2,2,1-vægtede gennemsnit af de SCL-værdier som forfatterne benytter er vist i søjle 4 på Tabel 1: 1/8*10.6 +2/8*11.6 +2/8*10.3 +2/8*10.0 +1/8*10.5 = 10.61 og 1/8*11.0 +2/8*11.0 +2/8*9.7 +2/8*10.7 +1/8*10.9 = 10.59. Så det må konkluderes at den “stejle stigning” der vakte så stor opmærksomhed i 1991, hverken understøttes af de data der var tilgængelige i 1991 eller af de data der siden hen er fremkommet. Lassen og Friis-Christensen (2000) angiver de samme forkerte værdier (= 10.6, 10.6, 10.5, 10.1 år) som Thejll og Lassen (2000) for de opdaterede 1,2,2,2,1- filtrerede SCL’er og henleder tilmed særlig opmærksomheden på den ‘stejle stigning’ som de fejlbehæftede punkter 3 og 4 giver solcykluskurven og som umiddelbart synes at retfærdiggøre deres oprindelige beskrivelse i 1991-artiklen af en “slående god overensstemmelse” og “en tæt forbindelse mellem de to kurver i de opadgående trends fra 1900 til 1940 og siden 1970", dvs., over de sidste årtiers globale opvarmning. Tabel 1 samler de data der kræves for at læseren selv kan studere problemet lidt nærmere.
En graf der ofte optræder i den seneste tids klimadebat, er Fig. 3 i Thejll og Lassen (2000). Nedenstående Fig. 4 viser de to centrale kurver fra denne figur (dvs. temperaturkurven og de 1,2,1-filtrerede solcykluslængder) sammen med de 1,2,2,2,1-filtrerede solcykluslængder fra Fig. 2 i Friis-Christensen og Lassen (1991) suppleret med den ovennævnte (korrekte) opdatering af punkterne 1-4. Det ses at forfatterne, ved at forlade den oprindelige hypotese (der involverede de 1,2,2,2,1-filtrerede data) til fordel for en 1,2,1-filtrering, har opnået en noget bedre overensstemmelse med temperaturudviklingen - et eksempel på den generelle erfaring at kurvetilpasninger ofte kan forbedres ved at skifte udglatningsmetode efterhånden som nye observationer bliver tilgængelige.
Når man undersøger mulige korrelationer mellem to tidsserier er det altid klogt at anvende et tidsinterval der er så bredt som muligt. På Fig. 5 sammenlignes de 1,2,2,2,1- filtrerede minimum-minimum solcykluslængder med udglattede temperaturer på den Nordlige Halvkugle dækkende perioden fra 1400-1990. Temperaturserien er fremkommet ved at kombinere den rekonstruerede temperaturserie af Mann et al. [1998] med den moderne, termometerbaserede serie fra Hadley Centret (Combined land air and sea surface temperature anomalies for the Northern Hemisphere 1951-1998, på http://www.meto.gov.uk/ sec5/ CR_div/ Tempertr/ lsst_ vals _nh.html). SCL-værdierne på Fig. 5 kan findes i Tabel 1 i Lassen og Friis-Christensen (1995). SCL-data fra år 1610 til nu kan hentes på web-adressen: ftp://ftp.ngdc.noaa.gov/STP/SOLAR_DATA/SUNSPOT_NUMBERS/maxmin.new. Parametrene er i det væsentlige de samme som dem der er vist på Fig. 3.a, men dækker her en længere tidsperiode. Tilpasningen af solkurven til temperaturkurven er opnået ved lineær regression. Det ses at den lineære regression giver en langt dårligere overensstemmelse mellem solcykluskurven og den terrestriske temperaturkurve når man som her prøver at få kurverne til at stemme overens over en lang tidsperiode, hvor de hver for sig opviser mange specifikke karakteristika. Her er sandsynligheden for at opnå en god overensstemmelse ringe - medmindre der virkelig eksisterer en årsagssammenhæng. Den ramme der er indtegnet på Fig. 5 angiver variabelintervallerne på Fig. 3.a, dvs. den oprindelige figur i Friis-Christensen og Lassen (1991). Hvis man prøver at skalere de to kurvers ‘S-former’ inden for rammen således at tilpasningen bliver optimal (som det rent faktisk er gjort på Fig. 3.a), kræver det en skaleringsfaktor der samtidigt med den gode tilpasning inden for rammen giver en dårlig tilpasning uden for. Eksempelvis ville uoverensstemmelsen mellem solkurven og temperaturkurven omkring år 1600, hvor den ene har en ‘top’ samtidig med at den anden har en ‘dal’, blive forstærket kraftigt. Omvendt: Hvis man valgte at optimere kurvetilpasningen i et tidsinterval omkring 1600 så ville skaleringsfaktoren simpelthen skifte fortegn og derved omdanne ‘toppen’ på solkurven til en ‘dal’ som ville stemme fint overens med ‘dalen’ på temperaturkurven. Men nu ville overensstemmelsen mellem kurverne uden for det nye interval (bl.a. i det indrammede interval) blive dårlig.
Det skal lige bemærkes at Fig. 5 her kun tjener til kvalitativt at illustrere et generelt træk ved lineære regressioner. Derfor er det uden betydning at de to temperaturserier der her er sammenføjet har forskellige referenceperioder og at dette i nærværende sammenhæng kun er søgt kompenseret ved en simpel additiv nulpunktskorrektion.
2.4 “Solcykluslængder korrelerer stærkt med overfladetemperaturen over land på den Nordlige Halvkugle (1995)”
I 1995 offentliggjorde Lassen og Friis-Christensen en ajourført og udvidet udgave af deres Science-artikel fra 1991. Dens centrale figur (Fig. 2 i deres artikel) vises nedenfor som Fig. 6.a (som rekonstruktion). Kurven med cirklerne viser solcykluslængder. De to optrukne kurver viser to forskellige temperaturserier. Den originale figur kan let give det indtryk at der kun er tale om en enkelt temperaturkurve der strækker sig over hele intervallet. I virkeligheden er temperaturudviklingen dog repræsenteret ved to forskellige serier: En serie der spænder fra 1585-1866 og en anden der spænder fra 1862-1982, med et overlap fra 1862-66. De to kurver er på Fig. 7 vist (også optrukket ) i lidt større format. Her ses det tydeligt at der er tale om to forskellige serier der overlapper, og som i det tidsrum hvor de overlapper, er parallelforskudt i forhold til hinanden svarende til en lodret afstand på omkring 0.1 ºC. Denne ejendommelige forskydning skyldes at forfatterne har afbildet de to serier direkte som rå temperaturanomalier, dvs. uden at tage i betragtning at de er målt i forhold til to forskellige referenceperioder. Dette forhold er blevet diskuteret i detaljer af Laut og Gundermann (1998). De ældre temperaturer på Fig. 6.a stammer fra Groveman og Landsberg (1979a, 1979b, 1979c) som i 1979 offentliggjorde en temperaturrekonstruktion for perioden 1579-1880. Som referenceperiode valgte Groveman og Landsberg intervallet 1881-1975, idet de byggede på en temperaturserie der var offentliggjort af Borzenkova et al. (1976). Ved at kombinere deres egen rekonstruerede serie med Borzenkovas data kunne Groveman og Landsberg opstille en serie af anomalier der spændte fra 1579-1975. Denne serie er vist som Fig. 1 i Groveman og Landsberg (1979a). Figur 7 nedenfor viser et løbende 11-årsgennemsnit af denne Groveman / Landsberg / Borzenkova temperaturserie (den punkterede linje). Serien kunne have været anvendt umiddelbart af Lassen og Friis-Christensen (1995) i deres sammenligning mellem solcykluslængder og overfladetemperaturen, idet den dækker hele det tidsinterval for hvilket der forelå solcykluslængder. Men i stedet for at anvende disse indbyrdes konsistente data brugte Lassen og Friis-Christensen (1995) en kombination af to forskellige temperaturserier med hver sin referenceperiode og derfor også med hver sin temperaturskala:
(1) Serien fra 1585-1866 på deres graf er en noget forenklet udgave af et 11-års løbende gennemsnit af Groveman / Landsbergs rekonstruktion. Den er vist som den venstre temperaturkurve såvel på Fig. 6.a som på Fig. 7. Serien er - ejendommeligt nok - ikke et korrekt 11-års løbende gennemsnit sådan som forfatterne beskriver den i deres artikel. Som det ses på Fig. 7 afviger den fra det korrekte 11-års løbende gennemsnit derved at en del af oscillationerne er fjernet. Den nøjagtige karakter af disse beskæringer er uklar.
(2) De nyere temperaturer på Fig. 6.a (dvs. den højre temperaturkurve på Fig. 6.a og Fig. 7) stammer fra Jones et al. (1986), Jones (1988) og Jones et al. (1998) som er defineret med 1951-70 som referenceperiode. Denne kurve er meget lig Groveman / Landsberg / Borzenkova-serien, bortset fra den ovennævnte forskydning nedad på omkring 0.1 ºC. Forskydningen skyldes den omstændighed at gennemsnitstemperaturen for Jones-seriens referenceperiode (1951-1970) lå omkring 0.1oC højere end gennemsnitstemperaturen for den referenceperiode (1881-1975) som definerer Groveman / Landsberg / Borzenkovaserien. Det betyder at talværdierne for Jones’ data kommer til at ligge omkring 0.1 ºC lavere end for de tilsvarende Borzenkova-data, selv om de to seriers temperaturforløb - når de udtrykkes i samme skala - stort set er identiske. Den forskydning nedad af den højre temperaturkurve (med de nyere temperaturer) får rundt regnet en tredjedel af den globale opvarmning der er sket over det tidsinterval som grafen dækker, til at forsvinde. Derved forbedres temperaturkurvens overensstemmelse med solcykluskurven. Kombinationen af disse to temperaturserier udtrykt i forskellige temperaturskalaer skaber således et forkert indtryk af overensstemmelse mellem solaktivitet og temperaturen på Jorden ved tilsyneladende at mindske den observerede globale opvarmning.
En anden ejendommelighed der bidrager til den tilsyneladende gode overensstemmelse på Fig. 6.a mellem solcykluskurven og den globale opvarmning er at solcykluskurven er blevet ‘løftet’ i hele dens udstrækning således at den passer meget fint med de (sænkede) moderne Jones’-temperaturer. Den forbedrede overensstemmelse mellem kurverne på figurens højre side er imidlertid opnået på bekostning af overensstemmelsen på figurens venstre side. Her ses det at næsten alle solcykluspunkter svæver højt over temperaturkurven. Var der blevet anvendt en simpel lineær regression ville antallet af solcyklusværdier over og under temperaturkurven stort set have været det samme. Kurvetilpasningen er altså her foretaget manuelt hvorved der er fremkommet en god overensstemmelse i netop den tidsperiode hvor bidrag fra menneskeskabte drivhusgasser er mistænkt for at have spillet en væsentlig rolle.
Fig. 6.b viser en korrigeret udgave af Fig. 6.a hvor visse ændringer i databehandlingen er indført: (1) I stedet for at anvende to forskellige temperaturserier med talværdier angivet i hver sin temperaturskala anvendes Groveman / Landsberg / Borzenkova-serien i sin helhed. Her er alle data angivet i samme temperaturskala. (2) Tilpasningen mellem solcykluskurven og temperaturkurven er her opnået ved simpel lineær regression, dvs. uden efterfølgende manuel tilpasning. (3) For at undgå at en mulig sol/jord-korrelation kunne blive ‘kontamineret’ af en - i denne sammenhæng - uvedkommende faktor, nemlig et eventuelt menneskeskabt bidrag til den globale opvarmning, er kun data før 1850 taget med i den lineære regression. I tilfælde af at det skulle vise sig at data fra før 1850 rummer en betydelig korrelation mellem solcykluslængder og terrestriske temperaturer, ville man så kunne undersøge om overensstemmelsen - med de samme regressionskonstanter - også gjaldt data efter 1850. En god overensstemmelse også efter år 1850 ville da kunne tolkes som et stærkt indicium for at den menneskelige indflydelse måtte være ubetydelig og at temperaturforløbet i det væsentlige er styret af Solens aktivitet og i dag simpelthen følger samme før 1850. Imidlertid følger temperaturkurven, som det ses af Fig. 6.b, ikke solcykluskurven, men stiger umiskendeligt over den.
2.5 “Solcykluslængder korrelerer stærkt med overfladetemperaturerne over land på den Nordlige Halvkugle (2000)”
I forbindelse med en artikel af Laut og Gundermann (2000a) der kritiserede Friis-Christensen og Lassen (1991), offentliggjorde disse forfattere en ‘svar-artikel’ (Lassen og Friis-Christensen 2000). I dette arbejde præsenterede de en ajourført udgave af deres 1995-resultater (vist som Fig. 6.a ovenfor). Den ajourførte udgave (Fig. 2 i deres nye artikel) er vist nedenfor som Fig. 8.a (en rekonstruktion). Det viser sig at det ikke er helt ligetil at gennemføre en kontrolberegning af denne figur da forfatterne kun giver en meget ufuldstændig forklaring på hvordan kurvetilpasningen er opnået. De nævner at de har indført vægtfaktorer på de observerede solcykluslængder der tager højde for at de ældre data er noget usikre. Imidlertid giver de ingen oplysninger om hvilke talværdier de har valgt for disse vægtfaktorer. En detaljeret analyse ved Laut og Gundermann (2000b) viser at forfatterne, for at nå frem til Fig. 2 i deres artikel (Fig. 8.a nedenfor) må have sat samtlige vægtfaktorer for data før år 1800 til nul eller til værdier meget nær ved nul. Fig. 8.b er opnået ved netop at sætte disse vægtfaktorer til nul. Det ses at Fig. 8.b stort set er identisk med Fig. 8.a. Dette valg af vægtfaktoren nul for alle soldata dækkende de første 230 år af solcyklusserien skal kommenteres: Fysiske data der fortjener en vægtfaktor på nul burde slet ikke vises på en graf af nærværende art. De må være alt for usikre til overhovedet at blive taget med i betragtning. Og hvis de af en eller anden grund alligevel tages med, så bør læseren advares imod at tillægge dem nogen værdi.
En anden interessant ændring i den ajourførte Fig. 8.a fra år 2000 i forhold til den originale Fig. 6.a fra år 1995 er det faktum at antallet af de data der dækker perioden 1850- 1980 er blevet fordoblet ved at tilføje 1,2,2,2,1-filtrerede maksimum-maksimum cykluslængder til de minimum-minimum cykluslængder som oprindeligt blev anvendt. Her skal det bemærkes at maksimum-maksimum cykluslængder i mange analyser (det gælder således 1995-artiklen) ikke anvendes fordi de anses for at være mindre nøjagtige. Ved denne fordobling af datapunkter inden for et specifikt interval fordobles også den matematiske vægt hvormed dette interval indgår i den lineære regression. Det medfører en kurvetilpasning der optimerer overensstemmelsen af de to ‘S-formede’ afsnit på hhv. solcykluskurven og temperaturkurven (som også er omtalt ovenfor i forbindelse med Fig. 5) på bekostning af tilpasningen i resten af kurvernes forløb. Da der er en begrundet mistanke om at temperaturerne netop på det ‘S-formede’ afsnit er stærk påvirket af menneskeskabte drivhusgasser, risikerer man at en eventuel korrelation der påvises på denne måde snarere skyldes en tilfældig covarians mellem solaktiviteten og en stigende menneskelig aktivitet (startende med den industrielle revolution) frem for en påvirkning af Jordens klima ved processer på Solen.
Nedenstående Fig. 8.c er baseret på praktisk taget de samme data som Fig. 8.a, idet der dog er foretaget følgende ændringer i databehandlingen: (1) Der er ikke set bort fra de første 230 års solcykluslængder. (2) Antallet af datapunkter mellem 1850 og 1980 er ikke blevet fordoblet. (3) Den lineære regression er blevet indskrænket til at omfatte data fra før 1850 for hvilke en evt. påvirkning fra menneskeskabte drivhusgasser endnu kan anses for at være relativ beskeden. (4) Alle de anvendte data har fået tildelt samme vægtfaktor i den lineære regression.
3. KONKLUSION
Flere af de figurer der diskuteres ovenfor har påkaldt sig stor opmærksomhed verden over, såvel i videnskabelige sammenhænge som i den løbende offentlige diskussion om muligheden af menneskeskabte klimaændringer. Jeg har ovenfor søgt at vise at de er fremkommet ved en ukorrekt databehandling. Da erkendelsen af at de ikke giver et korrekt billede af den fysiske virkelighed, stadigvæk ikke er særlig udbredt har jeg fundet det på sin plads at offentliggøre nærværende kritiske analyse.
Hvad angår den række nyere undersøgelser der tyder på at variationer i sollysets indhold af ultraviolet stråling måske påvirker Jordens klima ved at modulere temperaturen i stratosfæren og derved påvirke luftcirkulationen i troposfæren (Bond et al. 2001, Haigh 1996, 2001, Shindell et 1999, 2001) så er det meget vel muligt at man her er ved at have identificeret nogle afgørende fysiske klimamekanismer for sol-jordvekselvirkningen. Imidlertid er yderligere analyser nødvendige for at belyse og bekræfte deres rolle.
Til sidst vil jeg gerne give udtryk for at jeg - frem for den ovenfor leverede kritik - langt hellere ville have præsenteret en positiv gennemgang af forfatternes hypoteser og resultater. Ikke mindst af personlige hensyn til alle parter. Men jeg vil også understrege at jeg anser korrektioner til videnskabelige artikler som en forpligtelse vi forskere har - både over for hinanden og over for resten af samfundet. Vi er - efter min mening - ikke blot forpligtet t il selv at levere sandfærdig information, men også til at gøre opmærksom på det, når videnskabelige artikler på væsentlige områder leverer misinformation.
NOTER
1 DMSP står for “Defence Meteorological Satellite Project”. Målingerne foretages med “Special Sensor Microwave/Imager (SSM/I)”. Der måles bl.a. hyppigheder af skyforekomster over oceanerne, og der registreres kun ‘vandskyer’, dvs. skyer der består af vanddråber. Den betydelige andel af skyer der indeholder iskrystaller detekteres altså ikke. Dens tolkningen af de målte mikrobølgedata er ikke verificeret ved sammenligning med synoptiske data (observationer med øjet). DMSP-dataene afviger dramatisk fra og ISCCP-data, selv om man sammenligninger DMSP-serien med ISCCP-data for skyer der kun består af vanddråber. Årsagen til afvigelsen er ikke forstået (se Kristiánsson og Kristiansen 2000). Mulige forklaringer er at sensorerne ikke kan skelne vandskyerne fra andre fænomener og instrumentdrift.
2 ISCCP står for “International Satellite Cloud Climatology Project” . Der foretages målinger af elektromagnetisk stråling i det infrarøde og synlige område. Måleinstrumenterne er anbragt om bord på geostationære og polare meteorologiske satellitter. Herved produceres der datasæt for det globale skydække og for skyernes fysiske egenskaber. Tolkningen af disse data er verificeret med synoptiske data. Projektet har publiceret forskellige dataserier med forskellig struktur. Serienummeret indgår i navnet. De serier der er benyttet på Fig. 1.a-c hedder således ISCCP C2 og ISCCP D2. Målingerne fra dette ISCCP anses generelt for at være de bedste data der eksisterer på området. Datasættet er produceret af Goddard Institute for Space Studies i New York, og distribueres frit fra NASA Langley Research Center, Distributed Active Archive Center, Hampton, Virginia, U.S.A.
REFERENCER
Bond, G., Kromer, B., Beer, J., Muscheler, R., Evans, M.N., Showers, W., Hoffmann, S., Lotti-Bond, R., Hajdas, I., Bonani, G., 2001. Persistent solar influence on North Atlantic climate during the Holocene. Science 294, 2130- 3136.
Borzenkova, I.I., Vinnikov, K.Ya., Spirina, L.P., Stekhnovskii, D.I., 1976. Variation of Northern Hemisphere Air Temperature from 1881 to 1975. Meteorologiya i Gidrologiya 7, 27-35.
Carslaw, K.S., Harrison, R.G., Kirkby, J., 2002. Cosmic Rays, Clouds, and Climate. Science 298, 1732-37.
DER SPIEGEL, 2. Juni 2001, pp. 196-201, viser Fig. 2 i Friis-Christensen og Lassen (1991), som i nærværende artikel er vist som Fig. 3.a.
Friis-Christensen, E., Lassen, K., 1991. Length of the solar cycle: An indicator of solar activity closely associated with climate. Science 254, 698-700.
Groveman, B.S., Landsberg, H.E., 1979a. Simulated northern hemisphere temperature departures 1579-1880. Geophysical Research Letters 6 (10), 767-769.
Groveman, B.S., Landsberg, H.E., 1979b. Reconstruction of northern hemisphere temperature: 1579-1880. Publication No. 79-181. University of Maryland.
Groveman, B.S., Landsberg, H.E. (1979c). Data Appendices to Publication No. 79-181. Publication No. 79-182. University of Maryland.
Haigh, J.D., 1996. The impact of Solar Variability on Climate. Science 272, 981-984.
Haigh, J.D., 2001. Climate variability and the influence of the Sun. Science 294, 2109-2111.
Jones, P.D., Raper, S.C.B., Bradley, R.S., Diaz, H.F., Kelly, P.M., Wigley, T.M.L., 1986. Northern hemisphere surface air temperature variations: 1851-1984. Journal of Climate and Applied Meteorology 25, 161-179.
Jones, P.D., 1988. Hemispheric surface air temperature variations: Recent trends and an update to 1987. Journal of Climate 1, 654-660.
Jones, P.D., Briffa, K.R., Tett, S.F.B., 1998. High-resolution palaeoclimatic records for the last millennium: interpretation, integration and comparison with General Circulation Model control-run temperatures. The Holocene 8 (4), 455-471.
Kernthaler, S., Toumi, R., Haigh, J., 1999. Some doubts concerning a link between cosmic ray fluxes and global cloudiness. Geophys. Res. Lett. 26, 863-865.
Kristjánsson, J.E., Kristiansen, J., 2000. Is there a cosmic ray signal in recent variations in global cloudiness and cloud radiative forcing? Journal of Geophysical Research 105 (D9) 11851-11863.
Kristjánsson, J.E., Staple, A., Kristiansen, J., 2002. A new look at possible connections between solar activity, clouds and climate. Geophysical Research Letters 29 (23) 2107-2110.
Lassen, K., Friis-Christensen, E., 1995. Variability of the solar cycle length during the past five centuries and the apparent association with terrestrial climate. Journal of Atmospheric and Solar-Terrestrial Physics 57 (8) 835-845.
Lassen, K., Friis-Christensen, E., 2000. Reply to the article “Solar cycle lengths and climate: A reference revisited” by P. Laut og J. Gundermann. J. Geophys. Res.-Space, 105 (A12) 27493-27495.
Laut, P., Gundermann, J., 1998. Solar cycle length hypothesis appears to support the IPCC on global warming. Journal of Atmospheric and Solar-Terrestrial Physics 60, 1719-1728
Laut, P., Gundermann, J., 2000a. Solar cycle lengths and climate: A reference revisited. Journal of Geophysical Research 105 (A12) 27489-92.
Laut, P., Gundermann, J., 2000b. Is there a correlation between solar cycle lengths and terrestrial temperatures? Old claims and new results. The First Solar and Space Weather Euroconference: The Solar Cycle and Terrestrial Climate. European Space Agency 189-191.
Mann, M.E., Bradley, R.S., Hughes, M.K., 1998. Globalscale temperature patterns and climate forcing over the past six centuries. Nature 392, 779-787.
Marsh, N.D., Svensmark, H., 2000. Low cloud properties influenced by cosmic rays. Physical Review Letters 85 (23) 5004-5007.
Marsh, N.D., Svensmark, H., 2002. GCR and ENSO trends in ISCCP-D2 low cloud properties. Journal of Geophysical Research. In press.
Shindell, D.T., Miller, R.L., Schmidt, G.A., Pandolfo, L., 1999. Simulation of recent northern winter climate trends by greenhouse-gas forcing. Nature 399, 452-455.
Shindell, D.T., Schmidt, G.A., Mann, M.E., Rind, D.,Waple, A., 2001. Solar Forcing of Regional Climate Change During the Maunder Minimum. Science 294, 2149-2152.
Svensmark, H., Friis-Christensen, E., 1997. Variation of cosmic ray flux and global cloud coverage - a missing link in solar-climate relationships. Journal of Atmospheric and Solar-Terrestrial Physics 59 (11), 1225-1232.
Svensmark, H., 1998. Influence of cosmic rays on Earth's climate. Physical Review Letters 22, 5027-5030.
Thejll, P., Lassen, K., 2000. Solar forcing of the Northern hemisphere land air temperature: New Data. Journal of Atmospheric and Solar-Terrestrial Physics 62, 1207-1213.
Udelhofen, P.M., Cess, R.D., 2001. Cloud cover variations over the United States: An influence of cosmic rays or solar variability? Geophys. Res. Lett. 28(13) 2617-2620.
Wagner, G., Livingstone, D.M., Masarik, J., Muschler, R., Beer, J., 2001. Some results relevant to the discussion of a possible link between cosmic rays and earth’s climate. J. Geophys. Res. 106, 3381-3387.
Yu, F., Turco, R.P., 2000. Ultrafine aerosol formation via ion-mediated nucleation. Geophysical Research Letters 27 (6), 883-886.
FIGURER

Tabel 1: En ajourført beregning af punkterne 1 - 4 på Fig. 3.a med påvisning af to væsentlige regnefejl i de numeriske beregninger i Lassen og Friis-Christensen (2000) og i Thejll og Lassen (2000).
I Friis-Christensen og Lassen (1991) var de sidste fire punkter på solcykluskurven (på Fig. 3.a markeret med numrene 1-4) afsat svarende til solcykluslængderne: 10.5, 10.3, 10.3 og 9.7 år. Da ordinataksen er valgt med orientering nedad afbildes denne række aftagende værdier som en stejl stigning på solcykluskurven. Denne stejle stigning giver en god overensstemmelse med temperaturkurven der afspejler de sidste årtiers kraftige globale opvarmning. Imidlertid hører punkterne 1-4 ikke hjemme på Fig. 3.a, idet de repræsenterer en anden type data end resten af kurven, dvs. de 20 forudgående punkter. Disse 20 punkter angiver 1,2,2,2,1-filtrerede data, dvs. kraftigt udglattede data, hvorimod punkterne 1 og 2 kun er delvist filtreret og punkterne 3 og 4 slet ikke er filtreret. Dette gør en forskel: Ikke-filtrerede solcyklusdata (dvs. de fysiske observationer uden udglatning) oscillerer voldsomt omkring den udglattede kurve. Som påvist af Laut og Gundermann (2000) skyldes den tilsyneladende fine overensstemmelse mellem solcykluskurven og de sidste årtiers globale opvarmning på Fig. 3.a ene og alene denne blanding af forskellige datatyper. Overensstemmelsen understøttes ikke af de fysiske observationer. Denne konklusion gælder såvel de data som er tilgængelige i dag som de data der var tilgængelige i 1991 da figuren først blev offentliggjort i en Science-artikel. I deres egen opdatering (Lassen og Friis-Christensen 2000) konstaterer forfatterne at “Med den information der er til rådighed i dag skulle de fire værdier have været 10.6, 10.6, 10.5 og 10.1" og “Substitution af de oprindelige data med de korrekte data ændrer imidlertid ikke indtrykket af en stejl stigning i solcykluskurven mellem 1970 og 1984". Disse konklusioner er imidlertid baseret på en regnefejl. Thejll og Lassen (2000) præsenterer de samme fire værdier (se søjle nr. 13 i ovenstående tabel) som resultatet af deres ajourføring der bygger på observerede (se søjle nr. 1 og 2) så vel som to forudsagte ekstremer for solpletantallet (se de sidste værdier i søjle nr. 1 og 2, trykt i kursiv). En korrekt beregning af de sidste to 1,2,2,2,1-vægtede gennemsnit giver de filtrerede værdier 10.61 og 10.59 (se søjle 12). Det kan man overbevise sig om ved simpelthen at regne efter, idet de af forfatterne anvendte SCL-værdier er opført i søjle 4: 1/8*10.6 +2/8*11.6 +2/8*10.3 +2/8*10.0 +1/8*10.5 = 10.61 og 1/8*11.0 +2/8*11.0 +2/8*9.7 +2/8*10.7 +1/8*10.9 = 10.59. Kontrolberegningen viser således at den ‘stejle stigning’ der præsenteres i begge artikler alene skyldes regnefejl i forfatternes numeriske beregninger. Fejlene berører udelukkende de to punkter nr. 3 og 4, som netop er dem der skaber den ‘stejle stigning’. Alle de øvrige numeriske resultater i deres ajourføring er korrekte. Den korrekte beregning med anvendelse af præcis de samme data (angivet i tabel 1 og på Fig. 2 hos Thejll og Lassen 2000) giver følgende resultater: 10.64, 10.56, 10.61 og 10.59 (se søjle nr. 12). Disse værdier udviser ikke noget spor af den postulerede ‘stejle stigning’.
I Tabel 1 er de vigtigste fejl fremhævet (se søjle nr. 13). For at gøre det lettere at sammenligne er tidspunktet, 1996.8, for solpletminimet som er anvendt af forfatterne bibeholdt selv om den observerede værdi er 1996.4 (se søjle 1).
Det skal bemærkes at værdierne fra den elektroniske digitalisering af figurerne (i søjlerne 6, 8 og 13) er angivet uden afrunding for ikke at indføre en ekstra kilde til usikkerhed.
Det skal også nævnes at grunden til at søjlerne 7 og 9 kun indeholder nyere værdier for hhv. de centrale år og SCL, er at det kun er disse der er medtaget i Table 1 i Thejll og Lassen (2000). Denne begrænsning betyder for øvrigt at tabellen ikke indeholder alle de SCL der er nødvendige for at kunne kontrollere punkterne på forfatternes Fig. 1 og Fig. 2 og fx påvise de to regnefejl. At der ikke er tale om at forfatterne har benyttet andre data end de NGDC-data der er angivet i søjlerne 1-4 i nærværende tabel fremgår af at alle de andre 1,2,1- og 1,2,2,2,1-gennemsnit på Fig. 1 og Fig. 2 er plottet med de værdier der opnås ved en korrekt beregning under benyttelse af disse NGDC-data.

Figur 1: (a) Jordens ‘totale skydække’ og intensiteten af galaktisk kosmisk stråling som iagttaget ved Climax, Colorado (tynd optrukken linje, normeret til maj May 1965). Talværdierne er opnået ved scanning og digitalisering af Fig. 1 i Svensmark (1998). Trekanterne repræsenterer skydata fra NIMBUS-7 CMATRIX projektet for den Sydlige Halvkugle over havene ekskl. troperne. Kvadraterne viser ISCCP C2 og ISCCP D2 skydata målt fra geostationære satellitter over havene ekskl. troperne. Romberne er DMSP data som - iflg. Svensmark - repræsenterer “totalt skydække over havene på den Sydlige Halvkugle”. Såvel trekanterne, kvadraterne som romberne repræsenterer iflg. forfatteren “Jordens totale skydække”. (b) En sammenligning af to datasæt: DMSP-data og ISCCP-data for ‘totalt skydække’ som vist i Kristjánsson and Kristiansen (2000). Kvadraterne viser ISCCP-data, mens de to linjestykker der hhv. dækker perioderne 1988-1990 og 1992-1998 og løber op mod figurens højre hjørne viser DMSP-data. Den relative indbyrdes placering af disse to kurver kan vælges ret vilkårligt, dels fordi en indbyrdes kalibrering af måleserier fra forskellige satellitprogrammer næsten aldrig kan foretages særlig nøjagtigt, dels fordi disse to kurver repræsenterer helt forskellige fysiske størrelser. Sidstnævnte forhold fremgår bl.a. af at ISCCP- og DMSP-kurverne har helt forskellige forløb. I modsætning til de ISCCP- og DMSP-data der er vist på Fig. 1.a repræsenterer skydataene på Fig. 1.b det samme geografiske område. Herved opnås der en meningsfuld sammenligning. Det ses at i de tidsintervaller hvor kurverne overlapper falder det ‘totale skydække’ angivet ved ISCCP-serien, mens DMSP-seriens værdier samtidigt stiger. Den samme forskel udviser den samlede trend for hhv. ISCCP- og DMSP-serien. Derfor kan det konkluderes: at hvis det er korrekt at ISCCP-serien beskriver ‘totalt skydække’, så kan DMSP-serien umuligt også repræsentere ‘totalt skydække’. Teksten “ISCCP – 23 %” angiver at der er trukket 23 procentpoint fra ISCCP-dataene for at bringe dem nogenlunde på niveau med DSMP-værdierne. (c) Her ses en korrigeret og ajourført udgave af Fig. 1.a. Kvadraterne repræsenterer ISCCP-data og den optrukne kurve viser intensiteten af galaktisk kosmisk stråling som målt ved Climax, Colorado, udglattet som hos Kristjánsson and Kristiansen (2000). Korrektionen består i at samtlige DMSP-data er fjernet idet de slet ikke repræsenterer ‘totalt skydække’ og derfor ikke hører hjemme i nærværende sammenhæng. Ajourføringen består i at nye data for ‘totalt skydække’ er tilføjet fra http://isccp.giss.nasa.gov/ climanal1.html (2001).

Figur 2: (a) Lavt skydække (tyk linje) og intensiteten af galaktisk kosmisk stråling som målt ved Huancayo (tynd linje) iflg. Marsh og Svensmark (2000). (b) Lavt skydække (tyk linje) og intensiteten af galaktisk kosmisk stråling som målt ved Huancayo (tynd linje) iflg. Kristjánsson et al. (2002). (c) Som på Fig. 2.b men udglattet for at trenden træder tydeligere frem.

Figur 3: (a) Solcykluslængder, SCL, (kurve med + tegn) og overfladetemperaturer over land på den Nordlige Halvkugle (kurve med * tegn). Her vises de værdier Friis-Christensen og Lassen præsenterede som Fig. 2 i deres oprindelige Science-artikel fra 1991 (i rekonstruktion). For en ordens skyld skal det lige bemærkes at SCL ikke er afsat ækvidistante. Det skyldes at de enten er afsat midt imellem to solpletminima eller to maksima, og da afstanden mellem disse varierer noget kommer ‘centerårene’ til at ligge noget uregelmæssigt. ‘Solkurvens’ første 20 punkter er 1,2,2,2,1-filtrede solcykluslængder, og dens sidste fire punkter (markeret 1-4) markerer solcykluslængder der kun er filtreret delvist (punkterne 1-2) eller slet ikke (punkterne 3-4). Den stejle stigning som de to sidste punkter udviser skyldes simpelthen at de er plottet direkte som observerede solcykluslængder, altså uden filtrering (eller udglatning), og at sådanne ikke-filtrerede solcykluslængder danner en kurve med voldsomme udsving op over og ned under den kraftigt udglattede kurve der dannes af de 1,2,2,2,1-filtrerede solcykluslængder. Punkterne 3 og 4 er simpelthen en del af et sådant udsving op over den udglattede kurve. Det er alene denne blanding af forskellige datatyper der skaber det fejlagtige indtryk at solcykluslængdernes udvikling i de senere årtier meget fint svarer til den observerede globale opvarmning. (b) Her ses hvordan kurven burde have været offentliggjort i 1991, uden sammenblanding af forskellige datatyper. Her er solcykluskurven udelukkende bestemt ved data som rent faktisk var observeret på dette tidspunkt. Det punkt der er markeret med ‘0' angiver den sidste korrekt 1,2,2,2,1-filtrerede værdi. (c) Dette er en ajourført udgave af solcykluskurven med de værdier der præsenteres i Lassen og Friis-Christensen (2000) samt Thejll og Lassen (2000). Lassen og Friis-Christensen gør især opmærksom på den ‘stejle stigning’ som kurvens to sidste punkter, 3 og 4, udviser og ser den som udtryk for at også den ajourførte solcykluskurve viser en fin overensstemmelse med den globale opvarmning. En kontrolberegning viser imidlertid at den stigning som punkterne 3 og 4 udviser, alene skyldes fejl i de numeriske beregninger. En korrekt gennemført beregning på grundlag af de data som specificeres i Thejll og Lassen fører til det flade kurveforløb der er vist på Fig. 3.d. Bortset fra punkterne 3 og 4 er alle andre talværdier (inkl. punkterne 1-2) hos Thejll og Lassen beregnet korrekt. Forfatterne har dog foretaget visse afrundinger, mens Fig. 3.d. er mere præcis. Dette forklarer de små afvigelser mellem kurverne som ses ved en sammenligning af Fig. 3.c og Fig. 3.d. (d) Her ses en (korrekt beregnet) opdatering af den oprindelige solcykluskurve (Fig. 3.a), nu med punkterne 1-4 beregnet under benyttelse af de samme observerede og forudsagte data som også anvendes af Thejll og Lassen (2000). Bemærk, at de nye solcyklusdata danner en flad kurve der ikke på nogen måde afspejler de seneste årtiers globale opvarmning.

Figur 4: Observerede temperaturer (tynd linje) og 1,2,1-filtrerede solcykluslængder (punkteret linje) som vist på Fig. 3 i Thejll og Lassen (2000). 1,2,2,2,1-filtrerede solcykluslængder som vist på Fig. 2 i Friis-Christensen og Lassen (1991) med de sidste fire punkter opdateret (tyk linje).

Figur 5: 1,2,2,2,1-filtrerede minimum-minimum solcykluslængder (kurven med de udfyldte cirkler) og temperaturerne på den Nordlige Halvkugle (kurven uden symboler). Fig. 5 viser i det væsentlige de samme fysiske størrelser som Fig. 3.a, men her er de sammenlignet over en længere tidsperiode. Bemærk at en lineær regression som regel giver en langt dårligere overensstemmelse mellem solcykluslængder og terrestriske data når sammenligningen udstrækkes over et længere tidsinterval hvor hver af kurverne indeholder et større antal specifikke detaljer. Den indsatte ramme markerer det interval som Fig. 3.a spænder over. Det er værd at bemærke at mens en indbyrdes skalering som den i Fig. 3.a benyttede, anvendt på Fig. 4, ville forbedre overensstemmelsen mellem de to kurvers ’S-faconer’ inden for rammen, ville den samtidig give en meget dårligere kurvetilpasning uden for rammen. Fx ville afvigelsen mellem solcykluskurvens ‘top’ og temperaturkurvens samtidige ‘dal’ omkring år 1600 forøges.

Figur 6: (a) 1,2,2,2,1-filtrerede minimum-minimum solcykluslængder (linje med udfyldte cirkler) og to forskellige serier for overfladetemperaturen over land på den Nordlige Halvkugle: Grovemann / Landsberg der løber fra 1585 til 1866 (punkteret linje) og Jones der løber fra 1862 til 1982 (optrukken linje). Kurverne overlapper i perioden fra 1862 til 1866, hvor de forløber stort set parallelt i en afstand på omkring 0.1 ºC. Den tilsyneladende gode overensstemmelse mellem de to temperaturkurver og solcykluskurven er opnået på følgende vis: (1) De to serier er afbildet i to forskellige temperaturskalaer. Herved sænkes den højre kurve ca. 0.1 ºC i forhold til den venstre kurve, og den globale opvarmning, over det tidsrum kurven spænder over, mindskes tilsyneladende med en tredjedel. (2) Forfatterne har løftet hele solcykluskurven så meget at den stemmer godt overens med den højre del af temperaturkurven. Denne tilpasning er sket på bekostning af de ældre data. Virkningen kan umiddelbart aflæses af figuren: Solcykluskurvens punkter ligger på venstre side af figuren gennemgående højt over temperaturkurven. Hvis tilpasningen var sket ved lineær regression ville nogle af dens punkter ligge over, nogle under temperaturkurven. (b) Her er solcykluskurven (linje med udfyldte cirkler) den samme som på Fig. 6.a, men de to forskellige temperaturserier med værdier angivet i hver sin temperaturskala er her erstattet af Groveman / Landsberg / Borzenkova-serien for 1579-1975 (optrukken linje), hvis værdier alle er angivet i samme temperaturskala. For at lette sammenligningen er Groveman / Landsberg / Borzenkova - kurven ajourført med nulpunktskorrigerede Jones-data for årene 1975-82 således at kurverne slutter i samme år. Kurvetilpasningen er her opnået ved simpel lineær regression, idet der dog kun er benyttet data fra før 1850. Dette er sket for at undgå at en eventuel Sol/Jord-korrelation ‘sløres’ af en temperaturpåvirkning fra de menneskeskabte drivhusgasser.

Figur 7: Den punkterede linje viser et 11-års løbende gennemsnit af Groveman / Landsberg / Borzenkovatemperaturserien 1579-1975 som præsenteret i Groveman og Landsberg (1979). Den tykke kurve til venstre viser en forenklet udgave af et 11-års løbende gennemsnit af Groveman / Landsberg / Borzenkovatemperaturserien fra 1585 til 1866 som er anvendt i Lassen og Friis-Christensen (1995). Kurvens nøjagtige definition er uklar da den ikke stemmer overens med forfatternes egen beskrivelse. Den tykke kurve til højre viser et 11-års løbende gennemsnit af en temperaturserie fra 1862 til 1982 publiceret af Jones et al. (1986), Jones (1988) og Jones et al. (1998). Jones’ temperaturkurve beskriver en temperaturudvikling som er meget lig den tilsvarende del af Groveman / Landsberg / Borzenkova-kurven, lige bortset fra at den er forskudt 0.1 ºC nedad fordi Jones’ serie anvender en anden temperaturskala med et højere nulpunkt. For at lette sammenligningen er Groveman / Landsberg / Borzenkova - kurven ajourført med nulpunktskorrigerede Jonesdata for årene 1975-82 således at kurverne slutter i samme år.

Figur 8: (a) Solcykluslængder (linje med cirkler) sammenlignet med overfladetemperaturer over land på den Nordlige Halvkugle som præsenteret i Lassen og Friis-Christensen (2000). Tætheden af soldata efter år 1850 er blevet fordoblet idet der her (foruden minimum-minimum solcykluslængderne) også er medtaget maksimum-maksimum solcykluslængder. Herved opnås der en god tilpasning med solcykluskurven over netop den tidsperiode hvor der er mistanke om at en menneskeskabt opvarmningstrend ligger overlejret over Jordens naturlige temperaturfluktuationer. De dele af temperaturkurven der ikke er påvirket af menneskeskabte drivhusgasser, opviser kun en dårlig overensstemmelse med solcykluskurven. Det betyder at den delvise overensstemmelse mellem kurverne, som figuren viser, måske er en følge af følgende to faktorer: (1) en vis, tilfældig overensstemmelse mellem solcykluskurvens form og den måde hvorpå menneskelig aktivitet har udviklet sig og (2) den omstændighed at der ved kurvetilpasningen stort set ikke tages hensyn til observationer der ligger før den industrielle revolution. Denne problematiske udnyttelse af de to kurvers ‘S-faconer’ illustreres også af Fig. 5 ovenfor, hvor solkurvens flade ‘S-facon’ kan skaleres op således at den stemmer fint overens med temperaturkurvens stejle ‘S-facon’ inden for den indsatte ramme. (b) Her ses resultatet af en kontrolberegning der blev gennemført for at finde ud af hvilke numeriske vægte Lassen og Friis-Christensen (2000) har tildelt de ældre solcyklusdata. Forfatterne oplyser nemlig ikke de af dem indførte talværdier, og det er derfor ikke umiddelbart muligt at reproducere deres resultater. Fig. 8.b er opnået (efter en række forgæves forsøg) ved at sætte vægtfaktoren for samtlige solcykluslængder fra før år 1800 til nul. Den herved opnåede figur er praktisk taget identisk med forfatternes egen Fig. 8.a. Deres valg af vægtfaktorer er derfor ækvivalent med at der er set bort fra samtlige soldata før år 1800. Hvis disse vægtfaktorer virkelig er sat til nul skal der mindes om at man i videnskabelig sammenhæng normalt vil udelade data der fortjener en vægtfaktor på nul. Når data er så upålidelige at der overhovedet ikke kan tages hensyn til dem i en lineær regression bør de nok slet ikke præsenteres på en graf sammen med gyldige fysiske data, eller i hvert fald ikke uden at læseren informeres herom og advares mod at tillægge dem nogen betydning. Den fremgangsmåde der anvendes i forbindelse med Fig. 8.a kan beskrives således: Først tvinges solcykluskurven og temperaturkurven til at stemme overens netop i perioden 1870-1960, hvor temperaturkurven kan være præget af en menneskeskabt global opvarmning. Og så præsenteres den fine overensstemmelse over denne periode (over kurvernes to ‘S-faconer’) som indikation på at den globale opvarmning skyldes Solen og ikke menneskelige aktiviteter. (c) Her er kurvetilpasningen af de samme data som på Fig. 8.a og Fig. 8.b foretaget ved lineær regression, idet dog den kunstige fordobling af data over ‘S-faconen’, ved tilføjelse af maksimum-maksimum solcykluslængder, er udeladt. De første 230 år af solcyklusserien er her medtaget og med samme vægt som de øvrige soldata. Her har de altså ikke fået tildelt vægtfaktoren nul. For at mindske faren for at en evt. korrelation mellem de solare og terrestriske data kan blive sløret af en mulig menneskeskabt opvarmning er kun data før 1850 anvendt i den lineære regression.
15. marts 2016, 22:37 0 kommentar(er) · 4350 fremvisninger
Kommentarer
Der er ikke skrevet kommentarer til denne artikel.
Deltag aktivt i debatten om artiklen Peter Laut: Solens aktivitet og Jordens klima:
Lignende indhold
| Artikler |
| Solen |
| Henrik Svensmark |
| Svensmark/Marsh: Solens indflydelse på jordens klima, 2000 |
| Nyheder | Dato |
| Solens aktivitet ikke årsag til global opvarmning | 13-05-2009 20:56 |
| Debatter | Svar | Seneste indlæg |
| Cepos og Svensmark - Solens og kosmisk strålings påvirkning af jordens klima | 4 | 04-07-2021 14:28 |
| Svensmark overdriver betydningen af egen forskning... | 15 | 22-10-2020 07:38 |
| Global opvarmning - drivhusgasser eller solaktivitet m.m. | 4 | 06-06-2019 14:31 |
| Usædvanlig sommer skyldes lav solaktivitet? | 31 | 20-08-2018 20:43 |
| Henrik Svensmark på Radio 24-7 | 91 | 21-03-2018 18:47 |